Calcule as integrais:
Passo 1
Ok, admito, essa integral assusta um pouco. Mas calma, isso acontece porque na verdade a gente acaba precisando de duas substituições. Veja bem, se escolhermos:
A integral vira:
O que é um pouco mais amigável, porque agora podemos visualizar uma necessidade de usar substituição trigonométrica! Pensando no seguinte triângulo auxiliar:
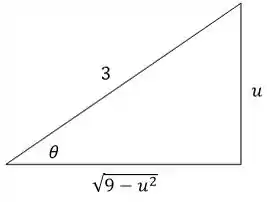
Podemos fazer a seguinte substituição trigonométrica:
Temos, ainda do triângulo auxiliar, que:
E portanto a integral vira:
Passo 2
Daqui em diante é mais tranquilo, só procedermos com as contas. Pra começar, dá pra cortar em cima e em baixo :
E opa! Na verdade já terminamos! O que falta falta mesmo é voltar pra variável original. Bem, como tínhamos do triângulo auxiliar:
Podemos usar funções trigonométricas inversas e conseguir isolar :
Mas não acabou! Não começamos com e sim com . Como a substituição era , ficamos com:
E feshow!