Lista de exercícios 10 – UFABC – Técnicas de integração– questão 12 item c
Calcule as integrais usando substituição trigonométrica. Esboce o triangulo retângulo.
c)
Passo 1
Faaaaaala, galera... Tranquileba?? Bora responder Aí essa questão?
Geralmente essas integrais são resolvidas por uma substituição trigonométrica, geralmente são:
E variantes dessa, o que nos libera uma gama de opções.
Veja que nesse caso temos uma variante podemos a partir dela chegar em algo parecido com o que foi dado em cima. Como?
Fatorando o 2:
E estamos agora mais próximos de alguma possível substituição e assim sai fácil facil. Consegue saber qual é? Cola junto
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Se você optou pela substituição com você acertou pois podemos achar alguma substituição com . Veja:
Façamos:
Um esquema no triangulo retângulo é:
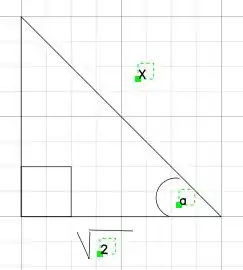
Derivando para obtermos dx:
PS: Anotem essas transformações, vamos usá-las ao final
Assim nossa integral fica:
Tirando os termos que se cortam:
Como dito antes, sabemos que . Assim:
Passo 3
Temos uma técnica de integração já conhecida para a integral de Ela aparece na tabela de técnicas de integração no fim dos livros de cálculos. É útil sempre a usarmos. Isto é:
Não podemos nos esquecer da bendita constante.
Lembra das nossas substituições?
E . assim
Resumindo:
Eu não disse que seria fácil? !
