Integração por Substituição Trigonométrica
Calcule
Passo 1
Olha o seguinte, esse cara dentro da raiz lembra o formato de um dos casos da integral por substituição trigonométrica:
Lança essa substituição na integral:
Pela Relação Fundamental da Trigonometria, .
Como eu defini na substituição, igual temos lá na teoria dessa matéria, que , então e :
Passo 2
Vamos usar uma relaçãozinha trigonométrica para esse cara:
Agora tem que fazer a substituição de volta. Para isso, temos que desenhar aquele triângulo clássico encaixando a nossa substituição original, com para um qualquer:
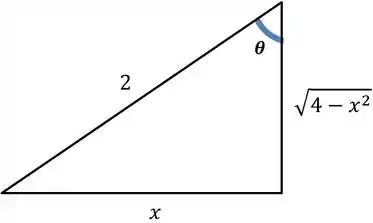
Nesse caso, e . Vamos escrever o resultado então:
Resposta
Exercícios de Livros Relacionados
Encontre o volume do sólido obtido pela rotação em torno da reta x = 1 da região sob a curva y = 1 - x 2 , 0 ≤ x ≤ 1 .
Calcule a integral usando a substituição trigonométrica indicada. Esboce e coloque legendas no triângulo retângulo associado. ∫ x 3 9 - x 2 d x ; x = 3 sin θ
Calcule a integral indefinida:int (x^2)/(sqrt(2 - x^2)) d x
Calcule a integral indefinida:int (5 x + 4)/(x^3 sqrt(x^2 + 1)) d x
Calcule a integralint (1)/(x^2 sqrt(4 x^2 - 1)) d x