Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Substituição Trigonométrica

Ver Teoria
Exercício 112123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFRJ, Lista 19 – AVA – Exercício 4

Demonstre a fórmula A = 1 2 r 2 θ para a área de um setor circular com raio r e ângulo central θ .

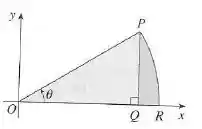
Passo 1

Primeiro, vamos dividir a figura em duas áreas, a primeira é a área com sombreado mais claro e podemos calcular sua área da seguinte forma

A 1 = 1 2 r cos ⁡ θ r sin ⁡ θ = 1 2 r 2 sin ⁡ θ cos ⁡ θ

A segunda área, primeiramente precisamos encontrar uma função que define a curva e depois integramos pra calcular a área, temos que a função que define um circulo é

x 2 + y 2 = r 2

Então, podemos isolar y da seguinte forma

y = r 2 - x 2

Então

A 2 = ∫ r cos ⁡ θ r r 2 - x 2   d x

Passo 2

Vamos resolver esta integral fazendo uma substituição trigonométrica, pra isso, seja

x = r cos ⁡ t

Diferenciando, temos que

d x = - r sin ⁡ t d t

Precisamos calcular os novos limites de integração

t i n f e r i o r : r cos ⁡ θ = r cos ⁡ t ∴ t = θ

t s u p e r i o r : r = r cos ⁡ t ∴ t = 0

Substituindo na integral, temos

∫ r cos ⁡ θ r r 2 - x 2   d x = ∫ θ 0 r 2 - r 2 cos 2 ⁡ t   - r sin ⁡ t d t = ∫ 0 θ r 2 ( 1 - cos 2 ⁡ t   r sin ⁡ t d t = ∫ 0 θ r 2 sin 2 ⁡ t r sin ⁡ t d t = ∫ 0 θ r 2 sin 2 ⁡ ( t ) d t = r 2 2 ∫ 0 θ 1 - cos ⁡ 2 t d t = r 2 2 t - 1 2 sin ⁡ 2 t 0 θ = r 2 2 t - sin ⁡ t cos ⁡ t 0 θ = r 2 2 θ - r 2 2 sin ⁡ θ cos ⁡ θ

Passo 3

Agora, para encontrar a área total, basta somarmos as áreas, então

A t = A 1 + A 2 = 1 2 r 2 sin ⁡ θ cos ⁡ θ + r 2 2 θ - 1 2 r 2 sin ⁡ θ cos ⁡ θ = 1 2 r 2 θ

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

Encontre o volume do sólido obtido pela rotação em torno da reta x = 1 da região sob a curva y = 1 - x 2 , 0 ≤ x ≤ 1 .
Calcule a integral usando a substituição trigonométrica indicada. Esboce e coloque legendas no triângulo retângulo associado. ∫ x 3 9 - x 2 d x ; x = 3 sin ⁡ θ
Calcule a integral indefinida:int (x^2)/(sqrt(2 - x^2)) d x
Calcule a integral indefinida:int (5 x + 4)/(x^3 sqrt(x^2 + 1)) d x
Calcule a integralint (1)/(x^2 sqrt(4 x^2 - 1)) d x