UFES– Cálculo 2 – P1 – Questão 2
Encontre a área da região delimitada pela hipérbole e pela reta .
Passo 1
Oi, tudo bem? O problema pediu para calcularmos a área delimitada pelas curvas
Vamos fazer um esboço dessa região:
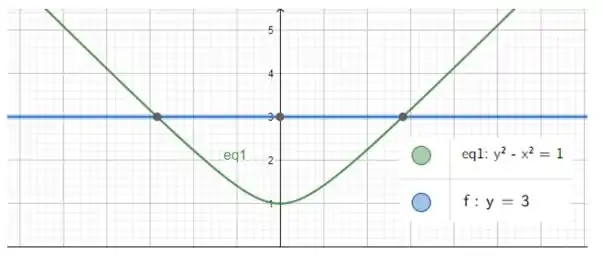
Os pontos onde as curvas se encontram são
Então a integral que representa essa área é:
Vamos resolver as integrais definidas em separado
Beleza?
Passo 2
A começando pela primeira:
Tranquilo até aqui?
vamos guardar esse resultado! Agora vamos calcular a segunda integral e depois juntar os resultados!
Passo 3
Vamos calcular a segunda:
Aqui vamos usar a substituição trigonométrica:
E vamos usar a identidade trigonométrica que Substituindo temos o seguinte:
Parece que ficou pior, mas é assim mesmo! Vamos fazer essa integral por partes! Separando essa secante ao cubo em uma multiplicação de (que será nosso ‘u’) e (será nosso ‘dv’):
Tudo bem até aqui?
Vamos agora juntar as integrantes ao cubo:
E por fim temos o resultado:
Beleza?
Nos resta agora voltar ao !
Fizemos a substituição de , então
e assim
Aí a integral que tínhamos:
Agora precisamos aplicar esses limites!
Passo 4
A segunda integral é
E agora vamos aplicar os limites e simplificar o que for possível:
Fazendo os cálculos aos pouquinhos! Calculando dentro das raízes e simplificando:
E agora podemos juntar os termos semelhantes:
Beleza?
mas podemos arrumar o argumento do logaritmo:
E aí substituindo essa expressão no logaritmo, podemos simplificar a potência:
Então nossa segunda integral tem esse valor aqui:
Tranquilo até aqui?
agora vamos juntar esse resultado com o resultado do passo 2, e colocar tudo na integral do passo 1!
Passo 5
Recapitulando: fizemos o esboço da região e encontramos essa integral para representar a área:
A primeira foi calculada no passo 2 e encontramos:
A segunda foi calculada nos passos 3 e 4 (sim, foi tenso kkk) e encontramos:
Agora é só juntar tudo:
Ufa! Terminamos! Então a região é
Espero ter ajudado! Até próxima!