UFRJ – Sem Campus – Cálculo 1 – Listas do AVA - Lista 19 – Questão 5UFRJ, Lista 19 – AVA – Exercício 5
A parábola divide o disco em duas partes. Encontre as áreas de ambas as partes.
Passo 1
Fala pessoal! Tudo certinho com vocês?
Nessa questão temos um disco, dado pela equação:
Ele está centrado na origem do plano cartesiano, e tem raio igual a .
E, temos também uma parábola, dada por:
Que possui ponto de mínimo em . (Lembra que (.
O objetivo do exercício é calcularmos as duas áreas em que a parábola dividiu o disco.
Como podemos fazer isso?
Podemos esboçar um gráfico pra visualizar o que esta acontecendo
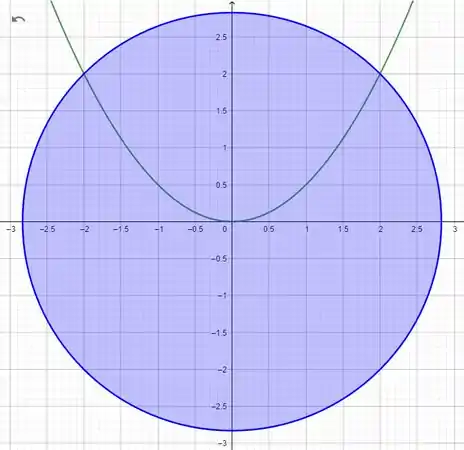
Com isso, podemos ver que os pontos de intersecçãoões entre as curvas, são os pontos , então, teremos esses limites de integração, agora, vamos deixar em função de
Agora, basta integrarmos
Vamos calcular cada integral separadamente
Passo 2
Calculando a primeira integral
Puts, ela parece bem chatinha né? Mas, tem um macete bem legal.
Quando temos dentro de raiz no numerador é uma boa tentar fazer uma substituição trigonométrica com seno ou cosseno. Isso porque muitas vezes aparece justamente a relação fundamental da trigonometria , e aí sumimos com a raiz. Se liga:
Vamos dizer que , diferenciando, temos que . Então, substituindo
Dissemos que , então
Na resolução da integral, vimos que
Então
Então, substituindo, ficamos com
Passo 3
Calculando a segunda integral
Logo
Para encontrarmos a outra área, basta fazermos
Prontinho galera! É isso aí, espero que vocês tenham curtido a solução!Até a próxima 😊