Sejam um intervalo aberto contendo e uma função derivável, com derivada contínua, tal que e . Calcule
Passo 1
Observa que quando a gente se depara com uma integral, a primeira coisa que a gente faz é observar se ela tem uma carinha que a gente já conhece. Observa que ali temos um .
Se você for observar isso lembra muito a integral que resolvemos pela substituição trigonométrica, né?
Como temos ela sendo do tipo
![]()
Chamareos de e de
Passo 2
O triângulo então que vamos trabalhar será dado por
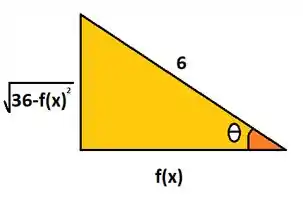
Com isso já podemos retornar pra nossa integral. Ficaremos com
Passo 3
Para resover a equação do temo macetada já a formulinha que nos dá
Aonde no nosso caso o
Passo 4
Próximo passo é então olhar pra nosso triângulo e trazer nosso resultado para função de novamente.
Lembrando que nós temos do enunciado.