Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Conservação do Momento Angular

Ver Teoria
Exercício 101123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Um aluno senta numa cadeira giratória com pesos na mão. A cadeira não apresenta atrito se for girada. Inicialmente ele faz um impulso e começa a girar com velocidade angular ω 1 . Nesse instante seu momento angular é L → 1 e seu momento de inércia I 1 . Em seguida ele fecha os braços, conforme mostra a figura, ficando assim com momento angular L → 2 , momento de inércia I 2 e velocidade angular ω 2 . Após o aluno começar a girar, o torque resultante externo é nulo.

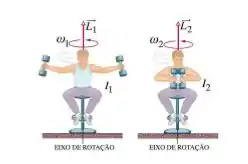
Analise as afirmativas abaixo:

I   ω 1 = ω 2

I I   L → 1 = L → 2

I I I   I 1 =   I 2

I V   I 1 > I 2

V   I 2 > I 1

V I   ω 1 > | ω 2 |

V I I   ω 2 > | ω 1 |

V I I I   L → 1 > | L → 2 |

I X   L → 1 < | L → 2 |

X   ω 1 ω 2 = I 1 I 2

X I   ω 1 ω 2 = I 2 I 1

Assinale a alternativa que contém apenas as VERDADEIRAS:

(a) I ,   I I   e   I I I

(b) I I ,   V I I   e   X I

(c) I I ,   I V ,   V I   e   X

(d) I V ,   I X ,   V I I   e   X I

(e) I I ,   I V ,   V I I   e   X I

(f) I I ,   V ,   V I I   e   X

(g) V ,   V I   e   V I I I

(h) I ,   I V   e   I X

(i) V ,   V I I   e   I X

(j) I I ,   V I I   e   X

(k) I I ,   I V   e   V I I

Passo 1

Como o torque externo é nulo e:

τ = d L d t

O momento angular se conserva. Isso nos diz que:

L a n t e s = L d e p o i s

I 1 ω 1 = I 2 ω 2

Temos que entender também que, ao encolher os braços, o aluno diminui seu momento de inércia, já que os alteres criavam componentes do tipo m R 2 .

Portanto:

I 1 > I 2

Com isso, concluímos também que:

ω 1 < ω 2

Estas afirmações feitas até aqui nos mostram que I I , I V , V I I e X I estão corretas.

Resposta

Letra (e)

Exercícios de Livros Relacionados

Um homem está em pé em uma plataforma que gira (sem atrito) com uma velocidade angular de 1,2 r e v / s ; seus braços estão abertos e ele segura um tijolo em cada mão. O momento de inércia do sistema
Na figura abaixo duas partinadoras com 50kg de massa, que se movem com uma velocidade escalar de 1,4m/s , se aproximam em trajetórias paralelas separadas por 3m . Uma das patinadoras carrega uma vara
Um patinador girando. Podemos considerar as mãos e os braços esticados para fora de um patinador que se prepara para girar como uma barra delgada cujo eixo de giro passa pelo seu centro de gravidade (
Uma barra uniforme de 0,0300 kg e comprimento de 0,400 m gira em um plano horizontal em torno de um eixo fixo passando em seu centro e perpendicular à barra. Dois pequenos anéis, cada um com massa de
Um pequeno inseto de 10,0 g está pousado sobre uma das extremidades de uma barra delgada e uniforme, que está inicialmente em repouso sobre uma mesa horizontal lisa. A outra extremidade da barra pivot