Exercícios Resolvidos de Conservação do Momento Angular

Ver Teoria

Exercício 109 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100

Enunciado

Uma bola de boliche de raio é lançada com velocidade sobre uma superfície plana horizontal, sem movimento rotacional. O coeficiente de atrito cinético entre a bola de boliche e a superfície é . Enquanto desliza, por causa do atrito com a superfície, a bola inicia um movimento rotacional, até que passa a descrever um movimento de rolamento, rolando sem deslizar.

Calcule a aceleração do centro de massa e a aceleração angular da bola enquanto ela desliza sobre a superfície.

Determine o instante de tempo no qual a bola passa a rolar sem deslizar.

Passo 1

Bem, temos uma bola de boliche que no instante encosta no chão começa a deslizar e a girar sobre a superfície. Depois de um instante ela passa apenas a girar sem deslizamento:

Enquanto a bola de boliche desliza (antes do ) ela tem duas acelerações: uma do centro de massa () e outra aceleração angular () porque também ela dá início ao movimento circulatório.

Passo 2

Para encontrar a aceleração do centro de massa, podemos olhar para o problema não rotacional (como se ela estivesse apenas deslizando). Nesse caso, as forças envolvidas no deslocamento da bolinha seriam...

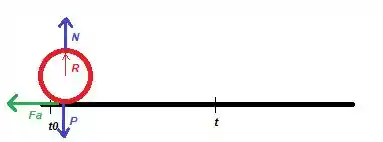
A força peso e a normal se cancelam, pois não há movimento na vertical, logo...

A única força na horizontal é a força de atrito e de acordo com a 2ª Lei de Newton...

Onde é a força resultante ()...

O motivo pelo qual eu inseri um menos foi apenas para indicar que a força de atrito está para a esquerda, ao tempo que a bola tem velocidade para a direita.

POW! Mas podemos calcular a força de atrito de acordo com as nossas teorias...

E como ...

Passo 3

POW! Sabemos pela cinemática rotacional que o torque na bola que a faz girar é igual á...

Onde é o momento de inércia rotacional. O momento para uma esfera é...

Então...

Por outro lado, a única força que causa torque na esfera é à força de atrito. Como a esfera gira ao redor do seu eixo e a distância da ao eixo de giro da esfera é ...