Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Conservação do Momento Angular

Ver Teoria
Exercício 102123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Momento angular

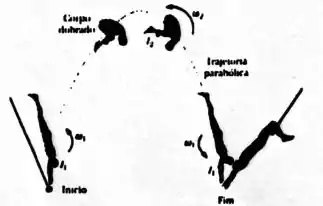
Durante um salto até o seu companheiro de número, um trapezista pretende fazer quatro cambalhotas (quatro voltas) em um intervalo de tempo ∆ t = 2 s . Durante o primeiro quarto da primeira cambalhota e durante o último quarto da última cambalhota, ele mantem o corpo esticado como na figura, com um momento de inércia I 1 = 20 k g . m 2 em relação ao centro de massa. Durante o resto do percurso ele mantém o corpo dobrado, com um momento de inércia I 2 = 4 k g . m 2 .

  1. Qual deve ser a velocidade ω 2 do trapezista em torno do eixo que passa pelo centro de massa quando ele está com o corpo dobrado?
  2. Qual deve ser o momento angular do trapezista em relação ao centro de massa durante o salto?
  3. Qual a razão entre as energias cinéticas de rotação, K 2 K 1 ?

Passo 1

a):

Bom galera, aqui a gente vai usar a conservação de momento angular, já que não há a atuação de nenhum torque externo no sistema.

É útil fazer isso primeiramente, pois assim gente vai poder escrever ω 1 , a velocidade inicial e final que é referente ao corpo esticado, em função de ω 2 :

I 1 ω 1 = I 2 ω 2 → ω 1 = I 2 I 1 ω 2 = 4 20 ω 2 = ω 2 5

Agora vamos usar o tempo pra terminar essa parada. O enunciado diz que o equilibrista tem que fazer todas as cambalhotas em 2 s . Porém, ele faz dois movimentos: O movimentos onde ele fica todo esticado, no inicio e no fim, e os movimentos nos quais ele fica encolhido. Então, a soma dos tempos desses dois estágios dão 2 s :

∆ t = ∆ t 1 + ∆ t 2

O primeiro pode ser calculado assim(levado-se em conta que o equilibrista, no inicio e no fim, percorre um quarto de volta e que ali a velocidade angular é ω 1 ) :

∆ t 1 = ∆ θ 1 = 2 . 1 4 . 2 π ω 1 = π ω 1

E como são 4 cambalhotas onde foram realizadas um quarto no fim e no inicio, podemos dizer que o restante do percurso vale:

∆ θ 2 = 4 - 2 . 1 4 2 π = 7 π

Então:

∆ t 2 = 7 π ω 2

Então:

∆ t = π ω 1 + 7 π ω 2

Usando:

ω 1 = ω 2 5

Então:

∆ t = 5 π ω 2 + 7 π ω 2 = 2

∴

12 π ω 2 = 2 → ω 2 = 6 π   r a d / s

Passo 2

b):

Pra calcular isso, basta a gente usar:

L = I 1 ω 1

Ou:

L = I 2 ω 2

Já que o momento não muda. Assim:

L = I 2 ω 2 = 4.6 π = 24 π   k g . m / s 2

Passo 3

c):

A gente vai ter que fazer:

K 2 K 1 = I 1 ω 1 2 2 I 2 ω 2 2 2 = I 1 ω 1 2 I 2 ω 2 2

Como:

ω 1 = ω 2 5

Então:

K 2 K 1 = 20 . ω 2 5 2 4 ω 2 2 = 20 . ω 2 2 25 4 ω 2 2 = 20 100 = 0,2  

Ou:

K 1 K 2 = 0,2 - 1 = 5

Resposta

a):

ω 2 = 6 π   r a d / s

b):

L = 24 π   k g . m / s 2

c):

K 2 K 1 = 0,2  

K 1 K 2 = 5

Exercícios de Livros Relacionados

Um homem está em pé em uma plataforma que gira (sem atrito) com uma velocidade angular de 1,2 r e v / s ; seus braços estão abertos e ele segura um tijolo em cada mão. O momento de inércia do sistema
Na figura abaixo duas partinadoras com 50kg de massa, que se movem com uma velocidade escalar de 1,4m/s , se aproximam em trajetórias paralelas separadas por 3m . Uma das patinadoras carrega uma vara
Um patinador girando. Podemos considerar as mãos e os braços esticados para fora de um patinador que se prepara para girar como uma barra delgada cujo eixo de giro passa pelo seu centro de gravidade (
Uma barra uniforme de 0,0300 kg e comprimento de 0,400 m gira em um plano horizontal em torno de um eixo fixo passando em seu centro e perpendicular à barra. Dois pequenos anéis, cada um com massa de
Um pequeno inseto de 10,0 g está pousado sobre uma das extremidades de uma barra delgada e uniforme, que está inicialmente em repouso sobre uma mesa horizontal lisa. A outra extremidade da barra pivot