[ENUNCIADO COMUM ÀS QUESTÕES 3 E 4]
Uma pessoa possui um braço de momento de inércia e agarra uma bola de massa e velocidade inicial perpendicular ao braço. A bola é agarrada no instante a uma distância do ponto , como mostra a Figura 1. Imediatamente após receptar a bola, o sistema braço + bola gira em torno de um eixo que passa perpendicularmente ao ponto com velocidade angular . Considere que todo o movimento ocorre em um plano horizontal e que a gravidade não é relevante para a situação descrita.
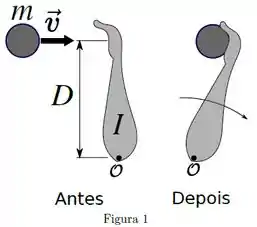
[QUESTÃO 4]
O módulo de logo antes da receptação é igual a:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Passo 1
Como não há forças externas ao sistema bola+braço atuando, também não temos nenhuma torque externo atuando:
Assim, o momento angular do sistema se conserva:
Vamos partir dessa conservação para encontrar a velocidade da bola antes da colisão.
Passo 2
O momento angular inicial será apenas o momento angular da bola:
O momento angular de uma partícula é dado pelo produto vetorial entre o vetor posição e o vetor momento liner :
seu módulo é dado por:
Mas dá uma olhada nessa imagem:
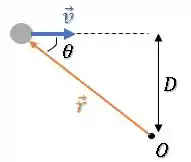
Ou seja, para qualquer instante antes da colisão (inclusive o instante exatamente antes), basta pegar a distância perpencidular ao vetor velocidade entre a partícula e o ponto :
Passo 3
Já para o momento angular final, temos o conjunto bola+braço em rotação.
Podemos calcular o momento angular de um sistema em rotação a partir de:
Entretanto, o momento de inércia é a soma do momento de inércia do braço que já conhecemos com o momento de inércia da bola à uma distânica do ponto de rotação:
Assim, ficamos com:
Passo 4
Conservando o momento angular, temos:
Isolando a velocidade da bola :
Substituindo os valores, temos:
Ficamos com a alternativa (d).
Resposta
Letra (d)