Uma haste de de comprimento e momento de inércia está montada horizontalmente (plano ) de modo a poder girar livremente no sentido horário em torno de um eixo na posição vertical. O eixo passa pelo centro de massa da haste.
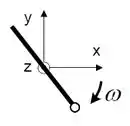
Em uma das suas extremidades está um dispositivo que lança bolinhas através de uma mola. O dispositivo tem massa desprezível e contém bolinha com momento d einércia em relação ao centro de massa da haste.
A haste é posta em rotação e alcança a velocidade angular . No instante em que o dispositivo passa pelo eixo positivo, ele lança a bolinha perpendicularmente à haste. Imediatamente após o lançamento, a velocidade angular da haste fica reduzida à metade.
- Determine a razão entre a massa da haste e a massa da bolinha.
- Determine o momento angular do sistema, em relação à origem do sistema de coordenadas, imediatamente antes do dispositivo lançar a bolinha. Determine a velocidade tangencial da bolinha imediatamente após o lançamento.
Passo 1
Letra a)
O problema nos dá os valores numéricos do momento de inércia da haste e da bola. Porém, a equação que dá cada um é sabida.
No caso da haste:
Onde é o comprimento da haste.
Já para a bolinha girando (note que o sistema de molas tem “massa desprezível”, então não precisamos nos preocupar com ele):
Onde é a distância da bolinha até o eixo de rotação, que no caso é a metade do comprimento da haste, .
Para acharmos a razão entre as massas, podemos dividir os momentos de inércia.
Por esse método, também seria possível encontrarmos a massa da haste e a massa da bolinha.
Passo 2
Letra b)
Para calcularmos o momento angular imediatamente antes do lançamento da bolinha, temos que somar o momento angular do dispositivo (lembrando que a parte da mola é desprezível, então só importa a bolinha) e da haste.
Porém, como a haste e a bolinha giram juntos
Porém, queremos o vetor momento angular. Neste caso, como a barrinha gira no sentido horário, temos que . Logo:
Passo 3
Para achar a velocidade tangencial da bolinha no instante após o lançamento, usamos a conservação do momento angular.
Note que queremos igualar os vetores momento angular antes e depois. No momento do lançamento, teremos o dispositivo na parte positiva do eixo , logo:
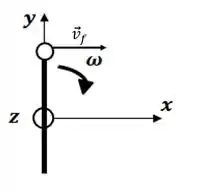
Para a velocidade angular da haste diminuir quando a bolinha é lançada, a bolinha deve ter sido lançada no sentido positivo do eixo (assim, a reação seria no sentido negativo, retardando a haste).
A parte do momento angular final devido à haste vai ser:
Já no caso da bolinha, agora ela não vai ter mais a mesma velocidade angular que a haste. Porém, a bolinha está seguindo no mesmo sentido que a ponta da haste, o que significa que sua velocidade angular também vai apontar no sentido negativo do eixo .
Assim:
Porém, pela cinemática do problema, podemos relacionar o módulo da velocidade angular da bolinha com o da velocidade linear.
Colocando tudo na conservação do momento angular
Como estão todos no mesmo sentido:
Temos então:
Resposta
Letra a)
Letra b)