Questão discursiva.
Uma criança, com massa de , corre em direção a um carrossel, de raio igual a e momento de inércia igual a , que pode girar em torno de um eixo sem atrito.
A criança se aproxima com velocidade constante de módulo igual a tangencialmente ao carrossel, que está inicialmente em repouso.
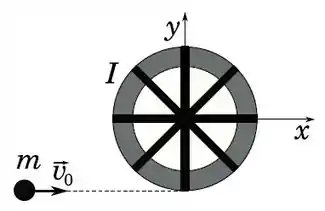
- Determine o módulo do momento angular da criança em relação ao eixo do carrossel, antes dessa pular sobre o carrossel. Considere a criança como uma partícula.
- o momento de inércia do sistema criança-carrossel;
- o módulo da velocidade angular e o sentido de rotação do sistema criança-carrossel.
A criança, então, pula e se agarra à lateral do carrossel e o sistema carrossel-criança passa a girar em conjunto com a mesma velocidade angular. Nesta situação, calcule:
Passo 1
Letra a)
O momento angular da criança em relação ao eixo do carrossel é:
Em módulo:
O é o ângulo entre os vetores, é o vetor de distância entre o eixo e a criança e é o momento linear da criança. O momento linear vai ser:
A massa da criança é e a velocidade dela .
A criança corre tangencialmente em direção ao carrossel e, quando chega lá, pula pra cima do carrossel.
Na iminência de pular no carrossel, a distância entre o eixo e a criança é:
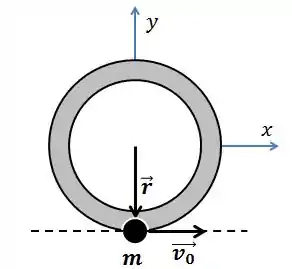
O ângulo entre e é e, por isso, o módulo do momento angular fica
Passo 2
Letra b)
O momento de inércia é o somatório
Podemos separar a parte relativa à criança, e ficaremos com:
Assim, para acharmos o momento de inércia do sistema carrossel-criança, nós somamos ao momento de inércia do carrossel o da criança, lembrando que .
Passo 3
Letra c)
Não há torques externos atuando no carrossel ou na criança, visto que além de não terem forças externas também não há atrito. Isso significa que o momento angular se conserva.
O momento angular inicial, logo antes da criança pular, é:
O momento angular depois da criança pular é dado pelo produto do momento de inércia com a velocidade angular.
Igualando os dois:
Igualando vetorialmente:
O que significa que o sentido da velocidade angular será o mesmo do momento angular inicial da criança. Como a criança vem em sentido anti-horário, o sistema carrossel-criança também vai girar no sentido anti-horário.
Resposta
Letra a)
Letra b)
Letra c)
O sistema gira no sentido anti-horário com velocidade angular .