UTFPR. Cálculo 2. AV1. 2022.1. Questão 5a.
Questão 5) Em quais pontos do plano cartesiano as funções abaixo são contínuas?
a)
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nessa questão foi dada uma função em que para diferente de ela se comporta como , já quando é igual a , ela se comporta como .
Com isso, temos que responder para quais pontos a função é contínua.
E agora! Como vamos responder essa pergunta?? 🤔
Perceba que em , a função possui uma descontinuidade já que se substituirmos e por , vamos obter uma indeterminação .
Pra isso, a função assume um valor em , no caso , para tapar o buraco feito pela
Indeterminação.
Preparado? Bora ver como vamos resolver esse problema! 😁
Passo 2
Queremos saber se quando admite o valor quando o buraco em quando é tapado ou se não contorna o problema da descontinuidade nesse ponto.
Pra isso, vamos calcular o limite de para quando tende a , ou seja
Podemos usar um método de aproximação através de curvas que passam pelo ponto , por exemplo a reta .
Substituindo por no nosso limite, temos
Como dividido por qualquer número é , então
Como sabemos, o limite de uma constante é a própria constante, ou seja
Tranquilo até aqui? 👀
Passo 3
Com o resultado obtido no passo anterior, podemos tirar uma conclusão:
Ou o limite de existe e é , ou o limite de não existe pois diverge.
Em qualquer um dos dois casos, a conclusão é que a função é descontínua em já que é nesse ponto, mas o seu limite ou é ou diverge!
Como o denominador só é se e forem , temos apenas um ponto de descontinuidade.
Assim, concluímos que é continua em todos os pontos, menos em !
Vamos visualizar o gráfico de pra observar o que estamos concluindo?
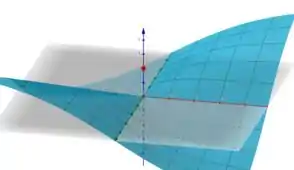
Assim podemos ver que tende a mas assume em !
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
Resposta
é continua em todos os pontos, menos em .