Questão discursiva – UFCG – Calculo diferencial e integral III – AV1 – questão 6 item b
Prove pela definição que
Passo 1
Faaaaaala, galera... Tranquileba?? Mogli na área 😊. Bora responder Aí essa questão?
A questão nos pede para calcularmos um limite de duas variáveis pela definição. Muitas pessoas temem o tal do limite pela definição, mas afinal, o que ele é?
Imagina que:
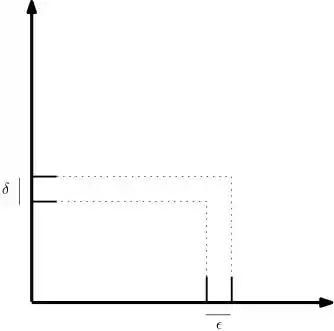
Imagina que temos um intervalo , de forma que para cada temos um associado a ele. Basicamente, para cada há um , isto é provar que o limite existe naquele ponto. De maneira mais matemática de falar:
Sendo o limite no ponto, e ( o valor das coordenadas no ponto.
Basicamente é isso, e alguns traquejos matemáticos. Bora lá?
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Assim, seja:
Substituindo e :
Agora aqui um traquejo, se a soma de termos quadráticos é menor que um valor, então concorda comigo que um termo isolado é com certeza menor ou igual que esse valor, assim:
Mas , logo:
E do mesmo modo:
e por que isso fizemos essas relações? Vamos ver mais pra frente que elas vão nos ajudar muito.
Agora vamos ver como é a relação para ?
Passo 3
Temos então:
Substituindo:
Mas saca só, podemos adicionar e subtrair , certo? Veja:
Veja que no final isso altera em nada. Podemos separar os módulos, sabendo que:
Assim:
Mas sabemos o que é e , lembra? Assim:
E logo:
Essa relação era a que procurávamos, porque aqui provamos que:
Continuando:
E provamos ao final que:
E enfim, chegamos.
E terminamos por aqui. Camarada. Obrigado por ter vindo até aqui comigo. Até a próxima!
Resposta
Provado nos passos acima