UFABC. Cálculo. Funções de Várias Variáveis. Lista 4 - Gradiente, Derivada Direcional e Derivadas Parciais de Ordem Superior. Questão 6.
6 - Suponha que a função de duas variáveis , diferenciável no ponto , satisfaz e , onde e . Determine:
a) ;
b) ;
c) A derivada direcional de em ao longo do vetor dado pelo segmento de reta orientado com ponto inicial e ponto final dado pela origem.
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Pode parecer que está faltando informações no enunciado, mas não se preocupe, está tudo certo com o enunciado!
Para essa questão vamos usar nossos poderes de resolução de derivada direcional para encontrar a derivada parcial de , com relação a no ponto , e também a derivada parcial de , com relação a no ponto , .
O que você vai dizer quando alguém perguntar o que é uma derivada direcional?
Certamente, você vai dizer “a derivada direcional representa a taxa de variação instantânea de uma função em um determinado ponto e em uma determinada direção” correto?
A gente tem uma formulinha para calcular a derivada direcional de , dada por
A derivada direcional de é resultado do produto interno do vetor formado pelas derivadas parciais de no ponto com o vetor direcional na sua forma unitária.
Está entendendo? Bora resolver.
Passo 2
Temos dois vetores e duas derivadas direcionais: para o vetor e para o vetor . Ambos no ponto .
Vamos montar a equação da derivada direcional para o vetor .
e podem ser escritos como e , respectivamente. já é um vetor unitário, então não precisamos mexer nele. Assim temos uma equação
Agora fazemos o mesmo para o vetor .
Assim como , também é um vetor unitário, então não precisamos mudar nada nele.
Temos duas equações e duas incógnitas, podemos montar um sistema e descobrir os valores de e !
Passo 3
temos o seguinte sistema:
Vamos multiplicar tudo por para tirar o denominador das equações
Podemos multiplicar a primeira equação por e subtrair com a segunda equação para zerar o da segunda equação.
Com isso, temos que
A derivada parcial de com relação a no ponto é . Substituindo esse valor na primeira equação, vamos encontrar
A derivada parcial de com relação a no ponto é !
Passo 4
No item c), devemos calcular a derivada direcional de , no ponto e na direção do vetor que começa no ponto e termina na origem.
Perceba que temos um tipo de quebra cabeça para descobrir o vetor.
Mas veja só, o ponto inicial do vetor é o ponto e o ponto final do vetor é a origem do sistema, ou seja:
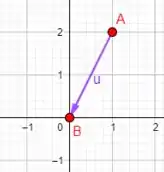
O vetor se desloca unidade no eixo e unidades no eixo , logo nosso vetor é dado como
Substituindo essas informações na formulinha da derivada direcional, temos
Lembrando que devemos usar o vetor em sua forma unitária, ou seja, dividindo ele mesmo pelo seu módulo.
Fazendo o produto interno, temos
Encontramos a derivada direcional de no ponto na direção do vetor como !
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
Resposta
a)
b)
c) ,