UFPE, Cálculo 2, 2°EE, 2012.2, questão 3
O relevo na vizinhança de um passo, numa cadeia de montanhas, é dado aproximadamente por , onde é a altitude relativa ao nível do passo.
- Qual a rota (direção) mais segura, associada a inclinação da estrada, para cruzar uma região circular em torno do passo?
- Determine a região segura para a construção de uma estrada pelo passo, se o material da mesma e o peso médio dos veículos determinam uma inclinação máxima de a fim de não haver deslizamento.
Passo 1
- A direção mais segura será aquela em que a altura tiver a menor taxa de variação possível, ou seja, zero. Como representa a altitude, teremos:
- A taxa de variação de um deslocamento na direção da inclinação é dada por . É só você pensar que taxa de variação é o , onde o vai ser o seno e o vai ser o cosseno. Beleza?
Passo 2
Na região circular em seu entorno, podemos fazer:
Calculando o gradiente:
Na vizinhança:
Passo 3
Vamos supor que a direção do vetor seja a de menor inclinação. Então, partindo nessa direção, o vetor terá as coordenadas:
Veja na figura a seguir:
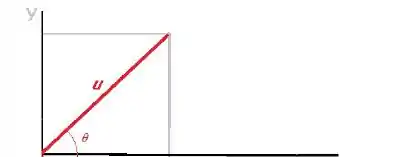
Como o gradiente tem coordenadas
Então, o ângulo entre esses dois vetores é , pois devido a segunda componente do gradiente, , sua componente é “negativa”. Veja a figura para melhor entender:
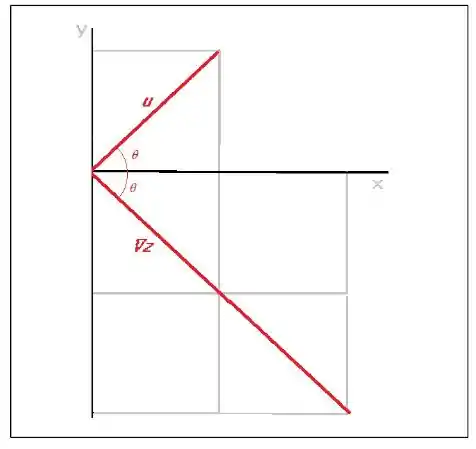
Passo 4
Sabendo que o módulo do gradiente é:
A derivada direcional fica:
Então, temos:
Então, a direção a ser tomada é
Passo 4
Passo 2
Já vimos que:
Como é a inclinação máxima, vamos ter:
Resposta
Exercícios de Livros Relacionados
Determine a derivada direcional da função no ponto dado na direção do vetor v. f x , y , z = x y z 3,2 , 6 v = - 1 ,- 2 ,2
Determine a derivada direcional da função no ponto dado na direção do vetor v → . f x , y = 1 + 2 x y , 3 ,4 ,v → = ( 4 ,- 3 )
14.1. É dado o mapa de contornos mostrando a pressão barométrica (em milímetros) às 7:00 horas da manhã do dia 12 de setembro de 1960, quando o Furacão Donna estava ativo. Estime o valor da função pre
Determine a derivada direcional da função no ponto dado na direção do vetor v → . f x , y = ln ( x 2 + y ² ) , 2 ,1 ,v → = ( - 1 ,2 ) ²
Determine a derivada direcional de f x , y , z = x y + y z + z x em P 1 , - 1,3 na direção de Q 2,4 , 5 .