6. Encontre:
e.
Passo 1
Oi, galerinha! Tudo bom? Aqui nós temos o seguinte limite para resolver:
O primeiro passo é substituir na função e ver se já chegamos em um resultado. Fica assim:
Repara que chegamos em logaritmo de zero, que é uma valor que existe. Porém aqui estamos resolvendo um limite, ou seja, vendo uma tendência.
Então vamos entender melhor o que significa esse e resolver a questão!
Passo 2
Quando substituímo na função, chegamos em . Mas repara que nós nos aproximamos de pela direita, ou seja, vamos ter valores próximo de zero, só que positivos dentro do logaritmo.
Além disso, temos que lembrar a cara de uma função logarítmica. No caso da nossa função , ela tem essa cara aqui
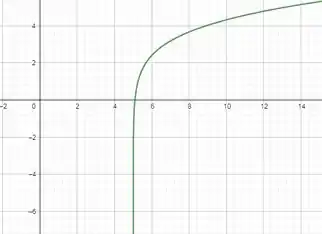
Repara que conforme nos aproximamos de , ela vai diminuindo e tendendo a .
De um modo geral, sempre que o argumento do logaritmo se aproximar de zero, a função vai para , ok?
Então temos que,
Prontinho!