UERJ, Sem Campus, Cálculo I, Listas de C1 - Profº Rubens Sucupira - Lista 3, Questão 50
Um avião está voando com velocidade constante a uma altitude de paralelamente ao solo.
Em um dado instante, um observador situado no solo observa que o ângulo de elevação do avião é de e está aumentando a uma taxa de . Calcule a velocidade do avião.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar a velocidade do avião, que está voando a uma altitude e tem um ângulo de observação . Esse ângulo varia a uma taxa . Nosso esqueminha mostra essa situação:
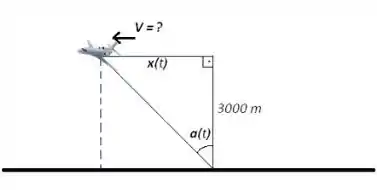
Como a velocidade é a taxa de variação da posição em relação ao tempo, o que nós queremos encontrar é . Então, como a gente quer saber a derivada da posição em relação ao tempo, precisamos encontrar uma expressão para essa posição , certo? Pra isso, vamos usar o esquema da figura acima e encontrar relações entre a distância horizontal e o ângulo .
Vamos lá!
Passo 2
Vamos começar usando a relação da tangente do ângulo no triângulo retângulo da figura no passo . Assim, temos:
Como o ângulo e a distância são consideradas funções do tempo, derivando essa expressão implicitamente, vamos ter:
Nós sabemos quem é porque o enunciado nos disse que o ângulo varia a uma taxa . Além disso, nós sabemos que quando , o ângulo de observação é .
Assim, isolando e substituindo os valores, temos:
E encontramos nosssa velocidade.
Valeu, galera! Até a próxima! 😉