Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Taxa Relacionada

Ver Teoria
Exercício 771234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757678798081828384858687888990919293949596979899100

Enunciado

UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº Ricardo Martins - Lista sobre Derivadas, Questão 8.6

Um reservatório de água no formato de um cone circular reto (vértice em baixo) está sendo enchido a uma taxa de 0,1 m 3 / s . O vértice está a 15 metros do topo e o raio do topo é de 10 metros. Com que velocidade o nível h da água está subindo no instante em que h = 5 ( h medindo de baixo para cima)?

Passo 1

Eaee!!! Belezinha? Bom... a questão nos dá um reservatório de água em formato de cone circular de 15 metros de altura e com raio superior de 10 metros, ou seja:

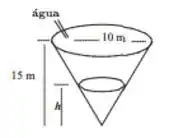
Onde h é a altura da água.

Queremos encontrar a velocidade com que a água está subindo no momento em que h = 5 metros.

Para isso, temos que saber que o volume V do cone é dado por:

V = π r 2 h 3

Onde r é o raio de acordo com a altura h .

Assim, temos que derivar essa equação e relação ao tempo para descobrirmos a velocidade da água.

Então vamos devagarinho aqui que vai dar certo!!

😉

Passo 2

Bom... primeiramente vamos relacionar h e r para não ficarmos utilizando duas variáveis.

Podemos fazer essa relação através de uma semelhança de triângulos. Assim, analisando a figura do Passo 1, temos:

15 r = 10 h ∴

r = 2 3 h

Assim, substituindo na equação do volume, temos:

V = π 2 3 h 2 h 3 ∴

V = 4 π h 3 27

Agora temos que derivar essa equação em função do tempo!!

Passo 3

Utilizando a regra da cadeia, temos:

d V d t = d V d h ∙ d h d t

Onde

d V d t = 0,1 m 3 / s

E

d V d h = 4 π h 2 9

Assim, substituindo e fazendo h = 5 , temos:

0,1 = 4 π h 2 9 * d h d t ∴

d h d t = 9 π 10 3   m / s

Entendeu direitinho? Responde aee ;)

Resposta

d h d t = 9 π 10 3   m / s

Exercícios de Livros Relacionados

20. Caminhão na estrada O gráfico a seguir mostra a posição de um caminhão que percorre uma estrada. O caminhão parte em t = 0 e retorna 15 h mais tarde, em t = 15.a. Use a técnica descrita no Exemplo
(a) Encontre a taxa de variação média da área de um círculo em relação ao seu raio r quando r varia de i 2a3i i2a2,5i i i 2a2,1 (b) Encontre a taxa de variação instantânea quando r = 2 (c) Mostre que
O número de células de levedura em uma cultura de laboratório aumenta rapidamente no início, mas eventualmente estabiliza. A população é modelada pela função n = f t = a 1 + b e - 0,7 t Em que t é med
O rendimento total recebido da venda de x carteiras é R x = 200 x - 1 3 x 2 c) Ache o rendimento real da venda da trigésima primeira carteira.
A quantidade de carga Q , em coulombs (C), que passa através de um ponto em um fio até o instante t (medido em segundos) é dada por Q t = t 3 - 2 t 2 + 6 t + 2 Encontre a corrente quando (a) t = 0,5 s