Uma escada de de comprimento está apoiada em um muro de de altura, conforme
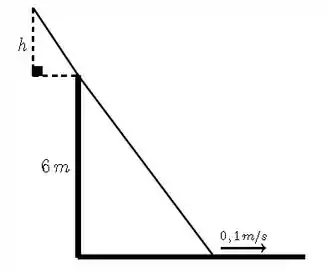
representado na figura. A base da escada desliza pelo chão, afastando-se do muro, com velocidade constante de . Determinar a taxa de variação instantânea da altura , indicada na figura, no instante em que a base da escada está a uma distância de do muro.
Passo 1
Vamos lá, a primeira coisa que a gente precisa fazer é olhar bem pra figura e saber o que está acontecendo, beleza? A escada está escorregando, então a ideia é essa aqui ó:
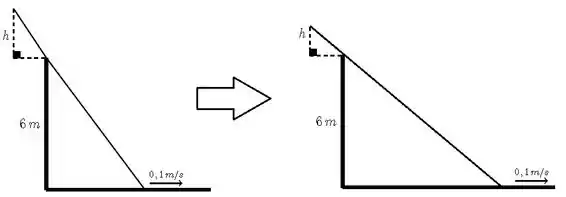
Então a gente sabe que está diminuindo com o tempo. Ok, beleza, o que a gente precisa agora é dar nome aos bois pra saber relacionar desconhecido com coisas conhecidas. Uma idéia é chamar assim:
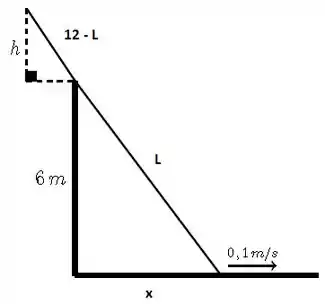
Agora, se você pensou em semelhança de triângulos, pensou certo! Os dois triângulos são triângulos retângulos, então podemos relacionar:
Passo 2
Ok, escrevemos como uma função de mas....e agora? A gente não sabe nada sobre ! Calma, podemos até não saber, mas olha a base do triângulo! Esse sim sabemos algo, sabemos a taxa com que a base aumenta! Sendo um triângulo retângulo:
A nossa altura então fica:
Agora basta a gente derivar em relação ao tempo galera! Saca só:
Passo 3
Agora é só a gente substituir os valores e partir pro abraço! Como o é pedido no instante em que a base da escada está a uma distância de do muro, temos que:
E da figura, temos que a taxa de variação da base do triângulo maior, ou seja, a taxa de afastamento da base da escada pro muro, é dada como:
Sendo assim: