Um homem se encontra em um barco a remo a 3km da costa e deseja chegar a uma cidade litorânea que está a 6 km em linha reta do ponto (na costa) mais próximo do barco. Ele rema a 4 km/h e caminha a 5 km/h. Onde ele deve aportar para chegar à cidade do no menor tempo possível.
Passo 1
E aí, gente!! Beleza? Nessas questões é sempre bom a gente primeiro tentar desenhar e escrever as funções que descrevem esse problema físico. Então sempre façam isso antes de sair resolvendo o problema.
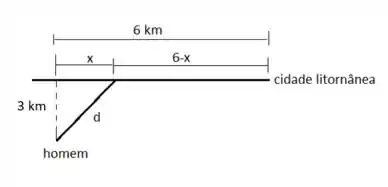
Vamos chamar de a distância na costa de onde ela aporta o barco e onde ela está. Como na figura
Passo 2
Assim, a distância que ele vai remar, vai ser feita por Pitágoras, que vai ser:
Como está no desenho.
O tempo que ele vai levar para fazer cada parte é a divisão da distância pela velocidade que ele tem.
Vamos ter que o tempo total vai ser:
Aqui, vamos ter que vai de , que é quando ele rema em linha reta até a costa e , que é quando ele rema em linha reta até a vila.
Passo 3
Para achar o tempo mínimo, temos que achar o ponto de mínimo de .
Para isso, temos que ver se existe algum extremo no intervalo de e comparar com os extremos do intervalo.
Vamos começar achando a derivada:
Para derivar aquela raiz, vamos escrevê-la em forma de potência:
Asism, teremos:
Não podemos esquecer de derivar o termo dentro da potência, por conta da regra da cadeia.
Vamos ter:
Multiplicando cruzado:
Elevando ao quadrado:
Simplificando:
Como é maior que , vamos pegar só
Passo 4
Agora, poderíamos verificar se ele é ponto de mínimo ou não. Mas aquela raiz vai ser bem ruim de trabalhar e a segunda derivada vai ser um porre. Então podemos antecipar isso e so comparar os extremos com esse valro de na função. O menor é o ponto de mínimo.
Vamos usar uma calculadora para ajudar as contas:
Então o ponto de mínimo é quando a distânciua for
Resposta
À km de distância, na costa, do ponto onde ele está.