Questão 3:
Considere o triângulo retângulo com catetos e . Sabemos que aumenta a uma taxa de , e que a área do triângulo permanece sempre igual a . A que taxa varia a hipotenusa do triângulo, quando ?
Passo 1
Estamos lidando aqui com uma questão de taxas relacionadas, certo? E em questões assim, o que eu faço sempre é colocar todas as equações necessárias para a resolução da questão, ou seja, todas as equações que relacionam com as variáveis.
Veja só:
É um triângulo retângulo para primeiro de conversa...
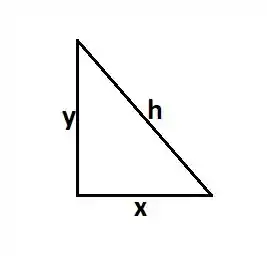
Então por Pitágoras, conseguimos informações sobre a hipotenusa ...
Outra função mencionada foi a área, e área de um triângulo retângulo é o produto dos catetos dividido por ...
Bem, essas são as equações que podemos tirar do enunciado que nos auxiliará. Bora ver como isso vai ficar?
Passo 2
Bem, com as equações em mãos, vamos ver o que podemos fazer para relacionar um pouco mais essas variáveis aí.
Foi-nos dito, que a área é sempre ...
Substituindo essa expressão na equação ...
Hmmm! Interessante essa relação que chegamos. Agora o que queremos?
Queremos a taxa de variação da hipotenusa com o tempo, ou seja...
Podemos então derivar a expressão que obtivemos implicitamente em relação a considerando e , ou seja, expressões que dependem implicitamente do tempo ...
Derivando o primeiro termo da igualdade aplicando a regra da cadeia...
Derivando o primeiro termo da soma também aplicando a regra da cadeia...
Sem se esquecer do último...
Nós queremos a , então basta ter , e , que matamos o problema !
Passo 3
E nós temos esses caras? SIM! Temos, ora bolas, o é a taxa de variação de no tempo, e esse valor foi dado...
é a coordenada do momento que a gente quer a taxa de variação, ou seja... .
Quanto a , ainda não temos, mas podemos encontrar rapidinho, já que sabemos que...
Logo .
Com esses três termos em mãos...
Esse menos significa apenas que a hipotenusa diminui o seu valor de cm a cada segundo nesse instante onde . :D