Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Taxa Relacionada

Ver Teoria
Exercício 461234567891011121314151617181920212223242526272829303132333435363738394041424344454748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Uma pedra é jogada de uma altura de 160   m . Um foco de luz está colocado também a 160   m de altura, a uma distância de 10   m da posição inicial da pedra. A altura da pedra após t segundos é A t = - 49 10 t 2 + 160 metros. Com que velocidade se moverá a sombra da pedra sobre o chão 2 segundos após a pedra ser jogada?

Passo 1

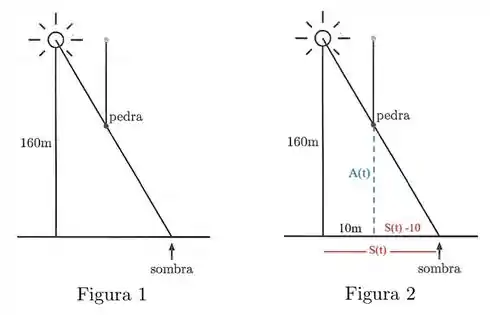
Chamaremos S ( t ) o deslocamento da sombra da pedra a partir da posição inicial x = 0 , onde se encontra o foco de luz. De acordo com a Figura 2, o deslocamento da sombra em relação a posição inicial da pedra será

S t - 10

Passo 2

Observe também na Figura 2 que possuímos dois triângulos que são semelhantes.

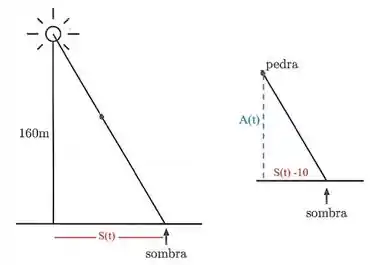
Por semelhança, podemos descobrir altura inicial da pedra, A ( t ) :

S ( t ) S t - 10 = 160 A ( t )

S ( t ) A ( t ) = 160 ( S t - 10 )

S ( t ) A ( t ) = 160 S t - 1600

S t A t - 160 S t = - 1600

- S t A t + 160 S t = 1600

S t ( 160 - A t ) = 1600

Passo 3

A questão pede a velocidade da sombra da pedra, isto é, S ' ( t ) . Vamos derivar a expressão acima, pois assim teremos uma equação com o termo que queremos descobrir.

S ' t ( 160 - A t ) + S ( t ) ( 0 - A ' t ) = 0

S ' t 160 - A t - S ( t ) A ' t = 0

Isolando no termo que precisamos descobrir:

S ' t 160 - A t = S ( t ) A ' t

S ' t = S t A ' t 160 - A t

Passo 4

Para obter a velocidade pedida, precisamos substituir t , A ( t ) , A ' ( t ) e S ( t ) na equação acima. Pelo enunciado, sabemos que

t = 2

Agora vamos descobrir A ( 2 ) .

A t = - 49 10 t 2 + 160

A 2 = - 49 10 2 2 + 160 = - 4 49 10 + 160 = - 98 5 + 160

Passo 5

Vamos achar A ' ( 2 ) .

A ' t = - 49 10 2 t + 0

A ' t = - 49 5 t

Agora

A ' 2 = - 49 5 2 = - 98 5

Passo 6

Só falta achar S ( 2 ) . Pela equação

S t ( 160 - A t ) = 1600

encontrada lá no Passo 2, podemos substituir A 2 = - 98 5 + 160

S 2 ( 160 - A 2 ) = 1600

S 2 = 1600 160 - A 2

S 2 = 1600 160 - ( - 98 5 + 160 )

S 2 = 1600 160 + 98 5 - 160

S 2 = 1600 98 5

S 2 = 4000 49

Passo 7

Agora falta apenas substituir t = 2 , A 2 = - 98 5 + 160 , A ' 2 = - 98 5 e S 2 = 4000 49 em

S ' t = S t A ' t 160 - A t

Vamos nessa.

S ' 2 = 4000 49 - 98 5 160 - - 98 5 + 160

S ' 2 = 4000 49 - 98 5 98 5 = - 4000 49   m / s

Resposta

- 4000 49   m / s

Exercícios de Livros Relacionados

20. Caminhão na estrada O gráfico a seguir mostra a posição de um caminhão que percorre uma estrada. O caminhão parte em t = 0 e retorna 15 h mais tarde, em t = 15.a. Use a técnica descrita no Exemplo
(a) Encontre a taxa de variação média da área de um círculo em relação ao seu raio r quando r varia de i 2a3i i2a2,5i i i 2a2,1 (b) Encontre a taxa de variação instantânea quando r = 2 (c) Mostre que
O número de células de levedura em uma cultura de laboratório aumenta rapidamente no início, mas eventualmente estabiliza. A população é modelada pela função n = f t = a 1 + b e - 0,7 t Em que t é med
O rendimento total recebido da venda de x carteiras é R x = 200 x - 1 3 x 2 c) Ache o rendimento real da venda da trigésima primeira carteira.
A quantidade de carga Q , em coulombs (C), que passa através de um ponto em um fio até o instante t (medido em segundos) é dada por Q t = t 3 - 2 t 2 + 6 t + 2 Encontre a corrente quando (a) t = 0,5 s