2. Um copo de papel tem a forma de um cone de de altura e de raio (no topo). Se for colocada água dentro do copo a uma taxa de , com que rapidez o nível da água se elevará quandro ela tiver de profundidade?
Passo 1
Oi, galerinha! Tudo bom? Aqui o que problema nos pede a taxa em que altura do nível de água aumenta com o tempo, e para isso, ele nos forneceu a taxa com a qual o copo vai enchendo. Ou seja, temos aqui um problema de taxa relacionada.
Então vamos começar entendendo o que esta acontecendo no sistema, para depois relacionar as taxas.
Bora lá!
Passo 2
Primeiro, vamos desenhar o nosso copo e calcular qual o volume dele.
Ele diz que o copo tem formato de um cone cuja a boca tem raio . Então vamos fazer esse cone invertido:
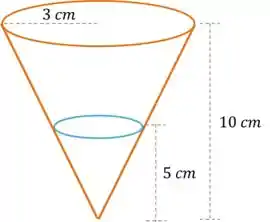
Temos que o volume do cone é dado, por
Opaaa! Repara que ao escrevermos essa fórmula, já estamos relacionando o volume com a altura.
Mas o problema pede a taxa de variação da altura. Então vamos derivar!
Passo 3
Temos a seguinte equação,
Como queremos a taxa de variação em relação ao tempo, vamos derivar
O problema quer saber exatamente quem é . Então vamos isolá-lo
Agora precisamos descobrir quem é e .
Passo 4
Galerinha, problema nos disse quem é , pois ele é justamente a velocidade com que o copo é enchido. Logo,
Agora precisamos achar quem é . Para isso, vamos fazer olhar a figura do cone e fazer uma semelhança de cones
Passo 5
Substituindo os dados encontrados na fórmula, ficamos com
Prontinho!