Um tanque tem de comprimento e sua seção transversal é sempre um triângulo equilátero, conforme a figura abaixo. Está sendo bombeada água para o interior do tanque a uma taxa de . Com que velocidade o nível da água estará subindo quando o conteúdo de água no tanque estiver com de profundidade?
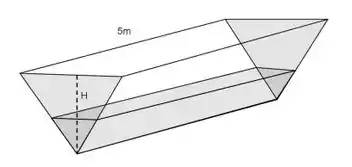
Passo 1
Bora lá. Pra começar, vamos pensar no seguinte. A água subindo, o volume aumenta, certo? Como o recipiente é um prisma de base triangular e a água assume o mesmo formato do prisma, então o volume de água vai ser:
Show de bola, mas tem coisa pra modelar ainda. Uma coisa já da pra adiantar galera, a altura . Esse prisma ta deitado, mas olha só, a altura é uma constante dada pelo problema! Nesse caso seria o comprimento de . E logo:
Falta modelar a área agora. Como temos um triângulo equilátero, saca só a nossa base.
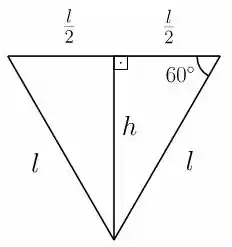
Como todo bom triângulo, a área vai ser:
Mas olha só, a altura do triângulo é a mesma coisa que a altura do nível de água! Como a questão fala disso, vamos escrever a área como uma função só da altura então, ok? Sendo assim, pela trigonometria, temos:
E pronto, terminamos de modelar a fórmula do volume, saca só. Primeiro, pra área do triângulo:
E pro volume:
Passo 2
Show de bola! Agora que sabemos como o volume de líquido funciona em função da altura de líquido, vamos ver as taxas. Galera, taxa lembra variação no tempo né? Então, sendo:
Derivando dos dois lados em função do tempo, temos, fazendo uma regra da cadeia:
No instante de tempo do enunciado, , temos algumas informações dadas por ele em! Elas são:
Substituindo:
E prontinho, essa é a taxa com a qual o nível de água aumenta!