UERJ, Sem Campus, Cálculo I, Listas de C1 - Profº Rubens Sucupira - Lista 3, Questão 56
Uma pipa, situada acima do solo, move-se horizontalmente a . Sabendo que a linha se encontra esticada, determine a taxa de variação do ângulo que essa linha faz com a horizontal no instante em que o comprimento da mesma for de .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar a variação do ângulo em relação ao tempo, que a linha da pipa faz com a horizontal. Nós sabemos que a pipa está a acima do solo e que se move com uma velocidade . E precisamos encontrar quando o comprimento da linha for igual a .
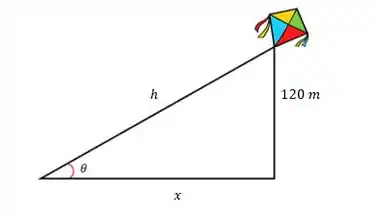
Então, vamos usar as relações trigonométricas do triângulo para encontra uma expressão para o ângulo , derivar essa expressão e encontrar nossa taxa .
Vamos lá!
Passo 2
Vamos começar usando a tangente do ângulo para escrever a relação entre os catetos e :
Derivando ambos os lados implicitamente em função do tempo , temos:
Isolando :
Passo 3
Agora vamos usar o teorema de Pitágoras no triângulo do passo e escrever:
Como , temos:
Fatorando, encontramos:
Passo 4
Agora vamos encontrar o valor da secante ao quadrado do ângulo, usando a identidade trigonométrica :
Usando as dimensões do triângulo e os valores que encontramos, temos:
Passo 5
Então, substituindo , e na derivada do ângulo, temos:
Simplificando:
Isso quer dizer que nosso ângulo varia a uma taxa de .
Valeu, galera! Até a próxima! 😉