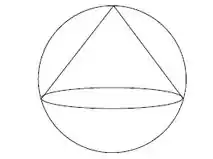
Um cone está inscrito em uma esfera conforme mostra figura abaixo. Se o raio da esfera está aumentando a uma taxa de e a altura do cone está aumentando a uma taxa de , com que taxa está aumentando o volume do cone no instante em que o raio da esfera mede e a altura do cone mede .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar a taxa de variação do volume do cone, que tem uma altura variável e que tá inscrito numa esfera de raio variável. Então, a gente precisa determinar quando o raio da esfera é , o raio do cone é e a altura do cone é .
Pra isso, nós vamos ligar um dos pontos da esfera até um dos pontos da base do cone, observando que se forma um triângulo retângulo de hipotenusa e catetos e . Assim, usando o teorema de Pitágoras, vamos ter a relação:
Dessa forma, usando os valores do enunciado vamos obter o valor de pra usar na equação da taxa de variação do volume do cone, que é derivada da equação .
Vamos lá!
Passo 2
Vamos começar pela relação que encontramos na nossa figura:
Substituindo e , dados pelo enunciado, temos:
Passo 3
Agora vamos pegar de novo nossa relação e derivar implicitamente:
E dividindo todo mundo por :
Mas o enunciado nos disse que raio da esfera está aumentando a uma taxa de e a altura do cone está aumentando a uma taxa de . Então, temos e . Além disso, nós temos , e , então substituindo todos os valores, vamos obter:
Passo 4
Nós vimos no passo que o volume do cone é dado por . Derivando essa equação implicitamente, usando a regra do produto, temos:
Então, substituindo os dados do enunciado e os valores que encontramos, temos:
Essa a taxa com que está aumentando o volume do cone no instante considerado.
Valeu, galera! Até a próxima! 😉