Um reservatório retangular de largura tem um painel interno que desliza com velocidade de afastamento .
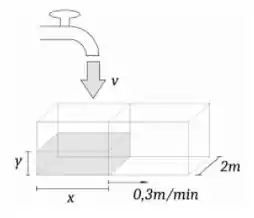
Sabendo-se que num determinado momento, o volume de água do reservatório da esquerda é e está crescendo à taxa de , determine se o nível de água está subindo ou descendo e com que velocidade nos seguintes casos:
a. No instante dado, o reservatório da esquerda tem comprimento
b. O reservatório da esquerda tem comprimento , naquele momento
Passo 1
Sabemos que o volume pode ser calculado da seguinte maneira:
Além disso, sabemos que a velocidade com que muda, isto é, a derivada de é
A taxa de variação do volume é de , ou seja:
Passo 2
Na letra é perguntado se o nível de água está subindo ou descendo e com que velocidade. Se queremos saber a velocidade com que diminui ou cresce, queremos saber a derivada de . Para achá-la, podemos derivar implicitamente a função do volume em função do tempo.
Passo 3
No instante considerado, sabemos que
Sabemos também que nesse instante . Como
Temos que
Ou seja, nesse instante a altura é de
Passo 4
Vamos juntar tudo isso na fórmula do passo 2, lembrando que
Então
Isso diz pra gente que no instante considerado a variação da altura é negativa! Logo o reservatório está descendo.
Passo 5
Para esse outro item a ideia é a mesma, só vão mudar os valores! Vem comigo:
Agora temos que
Então a altura nesse instante é de:
Passo 6
Com isso em mãos, vamos substituir na formulinha do passo 2
Isso diz pra gente que no instante considerado a variação da altura é positiva! Logo o reservatório está subindo.