UNICAMP – Cálculo 1 – Provas Antigas – P2 – 2022.1 - 5ª Vepertino – Questão 3
Um biólogo está em uma ponte sobre um rio e está inspecionando o rio com o auxílio de um drone. O drone mantém uma altura constante de com relação à ponte. O biólogo mantém o drone sobrevoando um trecho do rio em linha reta a uma velocidade constante de . Qual a taxa de variação da distância entre o biólogo e o drone quando a distância entre os dois for de ?
Passo 1
Eaeeee, belezinha??? Vamos juntos entender essa questão aqui!!
Primeiramente, vamos fazer um esquema visual aqui para podermos entender melhor a questão:
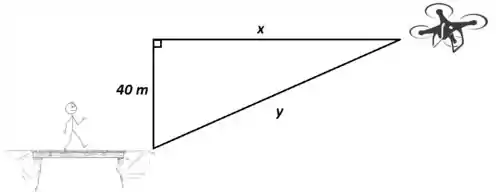
A questão ainda nos deu dois dados:
- O drone sobrevoa o trecho do rio em linha reta a uma velocidade constante de , ou seja:
- Pela figura acima, podemos ver que, pelo Teorema de Pitágoras:
Passo 2
Assim, derivando os dois lados da equação em relação ao tempo, temos:
Passo 3
A gente viu que e que . Assim, substituindo na equação do Passo 2, temos:
Então, quando a distância entre o biólogo e o drone for de , temos:
Entendeu direitinho? Responde aee ;)
