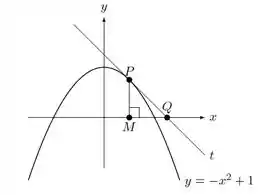
Considere a parábola na figura abaixo, onde a reta é tangente à parábola no primeiro quadrante em cada ponto . Sabendo que a taxa de variação da abscissa de (coordenada ) é de , determine a taxa de variação do lado do triângulo , quando o ponto de tangência é .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar a taxa de variação do lado do triângulo , quando o ponto de tangência é . Então, precisamos achar o valor de .
Se , a equação da reta tangente que passa por , vai ser:
Como , a equação de é na verdade:
O ponto é a interseção de com o eixo . Então, basta colocar na equação da reta para obter a coordenada de . Olhando no gráfico, nós vemos que . Com isso, conseguimos obter uma equação para , derivá-la e encontrar a taxa de variação do lado do triângulo.
Vamos lá!
Passo 2
Substituindo na equação , temos:
Isolando , vamos obter:
Então, . Como , a reta será:
Passo 3
Derivando essa relação, vamos obter a taxa de variação do lado:
Simplificando:
Mas no ponto , temos . Além disso, temos . Então, substituindo:
Que é a taxa de variação do lado do triângulo.
Valeu, galera! Até a próxima! 😉