Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Taxa Relacionada

Ver Teoria
Exercício 123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

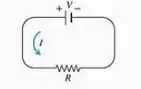
A voltagem V (volts), a corrente I (amperes) e a resistência R (ohms) de um circuito elétrico (veja a seguir) estão relacionadas entre si pela equação V = I R . Suponha que V esteja aumentando a uma taxa de 1 v o l t s / s , enquanto I está diminuindo a uma taxa de 1 / 3 A / s . Representaremos o tempo t em segundos.

a ) Qual é o valor de d V / d t ?

b ) Qual é o valor de d I / d t ?

c ) Qual equação relaciona d R / d t , d V / d t e d I / d t ?

d ) Encontre a taxa com a qual R está variando quando V = 12 e I = 2 A . R está aumentando ou diminuindo?

Passo 1

a)

Queremos saber o valor d V / d t , ou seja, o quanto a tensão varia no tempo. O próprio enunciado diz que a tensão está variando a uma taxa de 1 volt (tensão) por segundo (tempo). Então já temos essa informação:

d V d t = 1 v o l t s / s

Passo 2

b)

O próprio enunciado diz que a corrente está variando a uma taxa de 1 / 3 amper (corrente) por segundo (tempo). E ela está diminuindo, então a taxa de variação tem que ser negativa:

  d I d t = - 1 3 A / s

Passo 3

c)

Todas as taxas do enunciado estão em relação ao tempo. Para encontrá-la, derivamos implicitamente em relação ao tempo: V = I R ⟹ d V d t = d I d t ⋅ R + d R d t ⋅ I

Olhe lá! d R / d t , d I / d t e d V / d t estão nessa nova equação. Esta é a equação que os relaciona.

Passo 4

Quando V = 12 v o l t s , I = 2 A e, pelo enunciado, d V / d t = 1 v o l t s / s e d I / d t = 1 / 3 A / s :

d V d t = d I d t ⋅ R + d R d t ⋅ I ⟹ 1 = - 1 3 ⋅ R + d R d t ⋅ 2

Caramba! Para saber d R / d t temos que conhecer R , e agora? Simples, da primeira equação:

V = R I ⟹ 12 = 2 R ⟹ R = 6 Ω

Agora sim:

1 = - 1 3 ⋅ 6 + d R d t ⋅ 2

- 2 + 2 d R d t = 1

2 d R d t = 3

Portanto:

d R d t = 3 2 Ω / s

Que é positiva, então R está aumentando!

Resposta

a ) d V d t = 1 v o l t s / s

b ) d I d t = - 1 3 A / s

c )

d V d t = d I d t ⋅ R + d R d t ⋅ I

d ) d R d t = 3 2 Ω / s > 0 → R   e s t á   a u m e n t a n d o

Exercícios de Livros Relacionados

20. Caminhão na estrada O gráfico a seguir mostra a posição de um caminhão que percorre uma estrada. O caminhão parte em t = 0 e retorna 15 h mais tarde, em t = 15.a. Use a técnica descrita no Exemplo
(a) Encontre a taxa de variação média da área de um círculo em relação ao seu raio r quando r varia de i 2a3i i2a2,5i i i 2a2,1 (b) Encontre a taxa de variação instantânea quando r = 2 (c) Mostre que
O número de células de levedura em uma cultura de laboratório aumenta rapidamente no início, mas eventualmente estabiliza. A população é modelada pela função n = f t = a 1 + b e - 0,7 t Em que t é med
O rendimento total recebido da venda de x carteiras é R x = 200 x - 1 3 x 2 c) Ache o rendimento real da venda da trigésima primeira carteira.
A quantidade de carga Q , em coulombs (C), que passa através de um ponto em um fio até o instante t (medido em segundos) é dada por Q t = t 3 - 2 t 2 + 6 t + 2 Encontre a corrente quando (a) t = 0,5 s