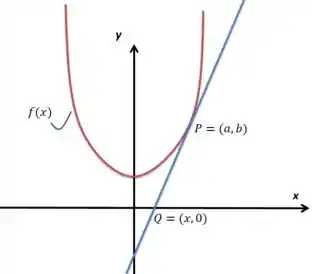
Sejam , com e um ponto sobre o gráfico de . Considere a reta tangente ao gráfico de no ponto e o ponto em que intercepta o eixo .
Determine, em termos da abscissa de , a abscissa do ponto .
Suponha que o ponto esteja sobre o gráfico de e que no instante em que sua abscissa esteja se deslocando a uma taxa de variação de unidades por segundo.
Determine a taxa de variação da abscissa do ponto nesse instante.
Seja o ângulo que a reta forma com o eixo . Determine a taxa de variação de nesse mesmo instante.
Passo 1
Para saber onde a reta tangente a corta o eixo nós precisamos antes de tudo descobrir que reta seria essa, né? Modelando a reta por , sendo o coeficiente angular da reta que valerá
Pois a reta tangente passa no ponto do gráfico, onde e .
Além disso, Lembramos que corresponderia à função de , ou seja, o ponto na verdade será:
Voltando ao coeficiente angular, temos que . Assim,
Enfim, se , e a reta será:
Passo 2
Tendo a reta, se queremos a abscissa de basta zerar , já que . Assim, achamos esse em função de :
Passo 3
A pergunta feita é, resumindo, qual o num dado instante em que e ? Vamos começar derivando o em função de :
Ora, num instante em que e :
Passo 4
Talvez você não lembre de primeira, mas o coeficiente angular de uma reta vale , onde esse seria o ângulo da reta com o eixo .
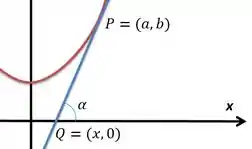
Ou seja, a tem o mesmo valor que a derivada da no ponto em que estamos estudando:
Vamos derivar dos dois lados e analisar como fica:
No instante temos e . Queremos então o valor de a partir do seguinte sistema:
Com e :
Passo 5
Temos uma relação trigonométrica entre tangente e secante, lembra?
Agora podemos substituir a na segunda equação e matar o valor de :