Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Taxa Relacionada

Ver Teoria
Exercício 631234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFRJ – Cálculo 1 – Lista 8 – Questão 2

Uma câmera de televisão no nível do solo está filmando a subida de um ônibus espacial que está subindo verticalmente de acordo com a equação s = 15 t 2 sendo s a altura e t o tempo. A câmera está a 600 m do local de lançamento. Encontre a taxa de variação da distância entre a câmera e a base do ônibus espacial, 10 segundos após o lançamento (suponha que a câmera e a base do ônibus estão no mesmo nível no tempo t = 0).

Passo 1

Opa, e aí galerinha!! Vamos tentar desenhar essa parada pra gente entender o que tá acontecendo?

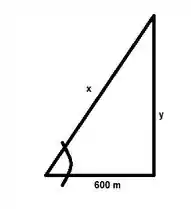
Bem, a distância entre câmera e ônibus espacial é dado pela distância x do nosso desenho, e de acordo com Pitágoras, temos que:

x 2 = 600 2 + y 2

x 2 = 360000 + 15 t 2

Queremos saber qual será a distância após 10 s do lançamento, certo? Então precisamos derivar isso aí!!!

Passo 2

Derivando em função do tempo, temos:

d d t x 2 = d d t 360000 + 15 t 2

2 x d x d t = 30 t

d x d t = 30 t x

Porém quem é x? Bem vimos quem é lá no passo 1 :

x = 600 2 + y 2

Logo,

d x d t = 30 t 600 2 + y 2

E y = s = 15 t 2

d x d t = 30 t 600 2 + 15 t 2 2 = 278,5   m / s

Resposta

d x d t = 278,5   m / s

Exercícios de Livros Relacionados

20. Caminhão na estrada O gráfico a seguir mostra a posição de um caminhão que percorre uma estrada. O caminhão parte em t = 0 e retorna 15 h mais tarde, em t = 15.a. Use a técnica descrita no Exemplo
(a) Encontre a taxa de variação média da área de um círculo em relação ao seu raio r quando r varia de i 2a3i i2a2,5i i i 2a2,1 (b) Encontre a taxa de variação instantânea quando r = 2 (c) Mostre que
O número de células de levedura em uma cultura de laboratório aumenta rapidamente no início, mas eventualmente estabiliza. A população é modelada pela função n = f t = a 1 + b e - 0,7 t Em que t é med
O rendimento total recebido da venda de x carteiras é R x = 200 x - 1 3 x 2 c) Ache o rendimento real da venda da trigésima primeira carteira.
A quantidade de carga Q , em coulombs (C), que passa através de um ponto em um fio até o instante t (medido em segundos) é dada por Q t = t 3 - 2 t 2 + 6 t + 2 Encontre a corrente quando (a) t = 0,5 s