Num determinado instante, um controlador de tráfego aéreo vê dois aviões na mesma altura voando a velocidades constantes, em trajetórias ortogonais que se cruzam num ponto P como descrito na figura ao lado. Neste instante, um dos aviões está a 150 milhas do ponto P e se aproxima de P a 450 milhas por hora, enquanto o outro está a 200 milhas do ponto P e se movendo a 600 milhas por hora, também em direção ao ponto P.
- Antes do ponto P, a distância entre os aviões está diminuindo? A que taxa?
- Os aviões correm risco de choque? Em caso afirmativo, quanto tempo o controlador tem para fazer com que um avião mude a sua trajetória?
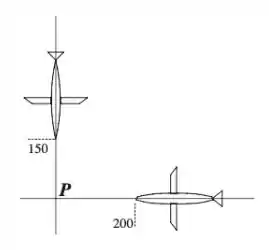
Passo 1
- A distância entre os aviões é a reta que liga os dois aviões formando um triangulo retângulo como abaixo
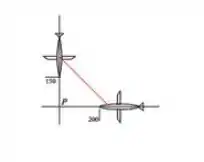
Essa distância está diminuindo conforme os aviões se aproximam de P. A taxa com que essa distância diminui é o que queremos encontrar. Para isso, temos que encontrar uma relação entre as variáveis envolvidas, que são as distâncias e de cada avião ao ponto P e d de um avião ao outro. Assim,
Passo 2
Derivando implicitamente a equação acima temos:
As distâncias d1 e d2 foram dadas no enunciado sendo 150 milhas e 200 milhas, respectivamente.
Logo,
Agora falta acharmos d1’ e d2’, mas veja só, essas não são as taxas das variações da distância em relação ao tempo de cada avião? E isso foi dado pelo enunciado.
Passo 3
Agora é só substituir e ser feliz!
Passo 4
(b) A equação que descreve a trajetória de cada avião é
Para o avião 1 isso pode ser escrito como sendo:
Para o avião 2:
Quando a gente vai ter colisão, então se igualarmos as duas equações poderemos verificar o seguinte:
O sinal negativo pode ser ignorado, porque ele está só indicando o sentindo negativo da posição: