UFSCAR – Cálculo 1 – Simulado 2 – Questão 1
Enche-se um reservatório, cuja forma é a de um cone circular reto, de água a uma taxa de . O vértice está a do topo e o raio é de . Com que velocidade o nível h da água está subindo no instante em que .
Passo 1
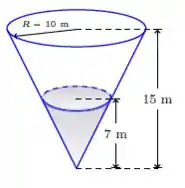
Fala galera, tudo bem? Essa é uma questão de taxa relacionada! Temos um cone e que está enchendo a uma taxa de . Aqui está um esboço desse reservatório
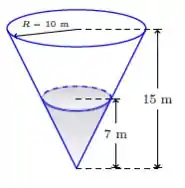
A questão pede a variação da altura da água quando a altura é . Temos a taxa de variação de seu volume, que é a derivada do volume e vale . Sabemos também que o volume do cone é dado por
Além disso, o enunciado diz que o raio do cone é . Então para resolver exercícios de taxa precisamos relacionar as grandezas!
Já temos a variação do volume – isso indica que precisamos derivar o volume! E queremos saber a variação da altura – então precisamos ter o volume apenas em termos da altura
E é isso! Olhando com mais carinho para o desenho vamos ter uma relação entre altura e raio, aí é só relacionar com o volume, derivar e partir para o abraço!
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Nossa missão agora é relacionar altura e raio! Olhando para o desenho
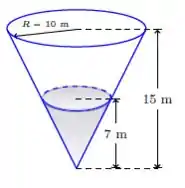
Assim:
Podemos então ter o volume apenas em função da altura:
Tudo bem até aqui?
Passo 3
Para achar a taxa de variação da altura, teremos que derivar implicitamente a equação que dá o volume em relação ao tempo:
E isolar a taxa de variação da altura
Beleza? Sabemos que o volume está variando segundo a taxa e queremos saber a taxa que a altura varia quando :
Então é isso pessoal! Terminamos!
Espero ter te ajudado!
=D