IME, Cálculo I, 2019, VE1, Q3
Considere um cubo inscrito numa esfera. Conforme o lado do cubo aumenta, a esfera também aumenta, de forma que o primeiro esteja sempre inscrito na segunda. Sabendo que o lado do cubo varia a uma taxa de , qual a taxa de variação do volume da esfera quando o cubo alcançar ?
Passo 1
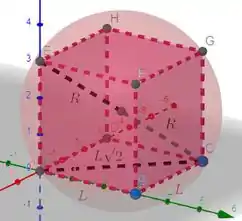
O volume da esfera é a grandeza a ser analisada portanto, considere:
Passo 2
Derivando o volume a regra da cadeia nos dá:
Substituindo:
Resposta
Exercícios de Livros Relacionados
20. Caminhão na estrada O gráfico a seguir mostra a posição de um caminhão que percorre uma estrada. O caminhão parte em t = 0 e retorna 15 h mais tarde, em t = 15.a. Use a técnica descrita no Exemplo
(a) Encontre a taxa de variação média da área de um círculo em relação ao seu raio r quando r varia de i 2a3i i2a2,5i i i 2a2,1 (b) Encontre a taxa de variação instantânea quando r = 2 (c) Mostre que
O número de células de levedura em uma cultura de laboratório aumenta rapidamente no início, mas eventualmente estabiliza. A população é modelada pela função n = f t = a 1 + b e - 0,7 t Em que t é med
O rendimento total recebido da venda de x carteiras é R x = 200 x - 1 3 x 2 c) Ache o rendimento real da venda da trigésima primeira carteira.
A quantidade de carga Q , em coulombs (C), que passa através de um ponto em um fio até o instante t (medido em segundos) é dada por Q t = t 3 - 2 t 2 + 6 t + 2 Encontre a corrente quando (a) t = 0,5 s