5) Um caminhão despeja cimento sobre o solo, que se acumula em um monte da forma de um cone, cuja altura é igual ao raio da base. Se o volume de cimento aumenta a uma taxa de , a que razão aumenta a área da base do monte formado pelo cimento, quando sua altura é de ?
Passo 1
A primeira coisa que devemos fazer em questões de taxas relacionadas como essas é prestar bastante atenção na geometria:
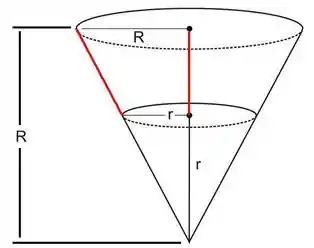
O cone grande é o formato final após todo o cimento ser despejado. Enquanto ele não chega em seu formato final, ele tem forma de um cone menor. Portanto o volume do cone de cimento pode ser descrito como:
Substituindo então temos:
Oras, o enunciado da pra gente a taxa com a qual o volume aumenta. Se a taxa é a variação com o tempo, então derivando em relação ao tempo, temos:
Substituindo a variação do volume pela taxa que conhecemos do enunciado de . Ficamos com:
Tem outro dado que conhecemos também do enunciado: o valor da altura no instante desejado. Como a altura é igual ao raio, do enunciado:
Passo 2
Ok, a princípio, ainda não chegamos a lugar nenhum. Afinal, a questão pede a taxa com a qual a área da base do monte formado pelo cimento aumenta. Como essa área é a área de um círculo, a fórmula dela a gente tira de letra:
Como quero taxa de variação, basta derivar em relação ao tempo, beleza? Ficamos com:
Opa, então o resultado do passo 1 não foi a toa né? Não mesmo meus caros. Afinal, mesmo que a gente substitua como fizemos antes, sem saber não ia ter como responder . Já que sabemos tudo, bora substituir então: