UERJ, Sem Campus, Cálculo I, Listas de C1 - Profº Rubens Sucupira - Lista 3, Questão 59
Um quadro com de altura está colocado numa parede vertical, sendo que sua base está a acima do nível dos olhos de um observador. Se o observador está se aproximando da parede a uma velocidade de , determine a taxa de variação da medida do ângulo de visão da pintura no instante em que o observador estiver a da parede.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar a taxa de variação do ângulo em relação ao tempo. Sabemos que o quadro tem de altura e está colocado na parede numa altura de acima dos olhos do observador. Observe a figura:
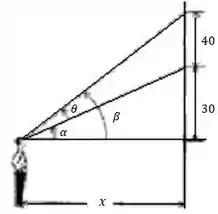
Sendo a distância do observador até a parede, observamos na figura que . Além disso, observando as relações trigonométricas desses ângulos, também vamos ter:
Substituindo essas relações em , temos:
Essa expressão que nós vamos derivar implicitamente em realação a , porque a distância também é uma função do tempo, e encontrar a taxa de variação da medida do ângulo de visão, , da pintura no instante em que o observador estiver a da parede.
Vamos lá!
Passo 2
Vamos começar escrevendo a derivada da nossa função:
Então, derivando em rela��ão a , teremos:
Agora vamos substituir a velocidade , que é negativa porque a medida que o observador se aproxima da parede, a distância diminui a uma taxa de , certo? Assim, temos:
Então, quando observado estiver a da parede, teremos e nossa taxa será:
Logo,
Valeu, galera! Até a próxima! 😉