Exercícios Resolvidos de Taxa Relacionada

Exercício 70 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100

Enunciado

UFABC – Cálculo 1 – Lista 2 – 14a

Uma pedra caiu dentro de um lago, produzindo uma ondulação circular que cresce a uma velocidade radial de 60 m/s. Encontre a taxa segundo conforme a qual a área dentro do círculo está crescendo depois de a) 1s b) 3s c) 5s. O que você pode concluir

Passo 1

E aí, gente!! Tudo bem? Vamos para mais um desafio?

Bora desenhar o que está acontecendo!!

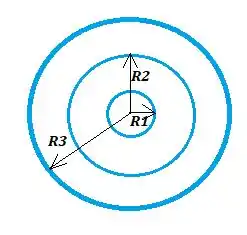
Note que com o tempo o raio dessa ondulação circular produzida tende a mudar de tamanho (aumentando tal que R1 d A / d t .

Passo 2

Sabe-se que a velocidade radial tem uma relação direta com a velocidade linear dada por:

A velocidade radial foi dada como 60, então:

Passo 3

A área do círculo é dada por

Podemos substituir , e ao final, temos:

Passo 4

Uma vez que temos agora a área em função do tempo, podemos calcular sua derivada nos respectivos tempos pedidos no enunciado.

Agora basta substituir .

A interpretação física é que, conforme o tempo passa, a área do círculo aumenta.

Resposta

Exercícios de Livros Relacionados

20. Caminhão na estrada O gráfico a seguir mostra a posição de um caminhão que percorre uma estrada. O caminhão parte em t = 0 e retorna 15 h mais tarde, em t = 15.a. Use a técnica descrita no Exemplo

(a) Encontre a taxa de variação média da área de um círculo em relação ao seu raio r quando r varia de i 2a3i i2a2,5i i i 2a2,1 (b) Encontre a taxa de variação instantânea quando r = 2 (c) Mostre que

O número de células de levedura em uma cultura de laboratório aumenta rapidamente no início, mas eventualmente estabiliza. A população é modelada pela função n = f t = a 1 + b e - 0,7 t Em que t é med

O rendimento total recebido da venda de x carteiras é R x = 200 x - 1 3 x 2 c) Ache o rendimento real da venda da trigésima primeira carteira.

A quantidade de carga Q , em coulombs (C), que passa através de um ponto em um fio até o instante t (medido em segundos) é dada por Q t = t 3 - 2 t 2 + 6 t + 2 Encontre a corrente quando (a) t = 0,5 s