Um farol, situado a uma distância de de uma muralha, completa voltas por minuto. Quando o facho de luz ilumina um ponto da muralha, situado a do farol, a velocidade com que o ponto de luz varre a muralha é de:
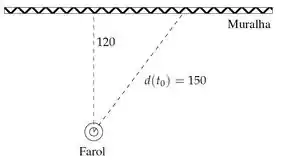
Passo 1
Olha, essa figura ajuda a entender. Mas essa aqui em baixo é um espetáculo, saca só:
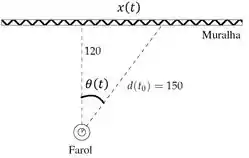
Esses nomes a mais vão ajudar a gente. Como o farol gira, tanto o ângulo quanto a base desse triângulo variam com o tempo. O que a questão pede na real é o quão rápido essa base aumenta ou diminui! Da trigonometria, temos que:
Como queremos a taxa de variação no tempo desse , derivando temos:
E como o farol está girando em uma velocidade constante de voltas () por minuto:
Show, mas olha só, a questão diz que em um determinado instante um ponto a do farol esta sendo iluminado. Representando esse instante então por , temos:
Vai faltar a gente achar então o ângulo nesse instante. Achando ele, encontramos a velocidade em que o ponto de luz varre a muralha nesse mesmo instante ().
Passo 2
Mesmo pareça doido obter informações de um instante específico, pensa aqui comigo: ué, esse instante não é exatamente o da foto? Certíssimo meus caros. E na imagem, olhando pelo triângulo, temos:
Sendo assim:
E a velocidade vai ser:
A resposta é a Letra