Considere a função
- Determine o polinômio de de grau centrado em de .
Passo 1
Item a) A única coisa que a gente tem que fazer aqui é aplicar a fórmula, se lembra dela?
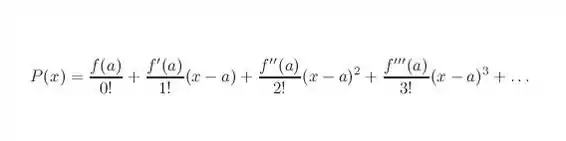
O no caso é , e queremos até o terceiro grau, logo teremos
Vamos encontrar essas derivadas aí?
Passo 2
A função que vamos derivar é essa
Calculando a primeira derivada
Agora a segunda lembrando de aplicar a regra da cadeia
Por fim, a terceira derivada aplicando a regra da cadeia e a regra do produto
Lembrando que e , podemos substituir o ponto nessas derivadas e obteremos
Jogando agora esse resultado no polinômio, vamos obter
Resposta
Item a)
Exercícios de Livros Relacionados
Demonstre que a série obtida no Exercício 11 representa x para todo x .
Encontre a série de Taylor de f centrada em 4 se f n 4 = - 1 n n ! 3 n n + 1 Qual é o raio de convergência da série de Taylor?
Encontre a série de Maclaurin f ( x ) usando a definição de uma série de Maclaurin. [Suponha que f tenha expansão em uma série de potências. Não mostre que R n → 0 .] Também encontre o raio de converg
Use a série binomial para expandir a função como uma série de potência. Diga o raio de convergência. 1 1 + x 4
Use uma série de Maclaurin na Tabela 1 para obter a série de Maclaurin da função dada. f x = sen π x