UFRJ, Sem Campus, Cálculo 1, Listas de C1 - Profº Jair - Primeira Edição V1.3, Questão 4.4.7
Um balão eleva-se verticalmente do solo à razão de . Quando o balão está a do solo, passa exatamente sob ele um automóvel viajando a velocidade de . Com que velocidade varia, (quatro) segundo após, a distância entre eles?
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar a taxa com que a dist��ncia entre um balão que se eleva verticalmente do solo e um carro viajando abaixo dele.
Vamos chamar de a posição do carro e a altura do balão. Então, o balão se eleva a uma taxa e o carro viaja a uma velocidade . A gente quer encontrar a taxa de variação da distância , quando o balão está em e .
Pra isso, vamos relacionar a distância entre eles através do teorema de Pitágoras, derivar a relação encontrada e substituir os valores dados no enunciado.
Vamos lá!
Passo 2
Vamos tentar visualizar a situação: o carro sai de baixo do balão em e o balão está inicialmente em . Depois de , com uma velocidade , nosso carro vai tá em . E o balão sobe de uma posição inicial , a uma velocidade no mesmo período de tempo, então temos:
Esquematizando o balão em e o carro em , temos:
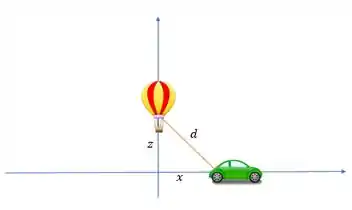
Então, pelo teorema de Pitágoras, vamos ter a distância sendo dada por:
Substituindo os valores para , temos:
Passo 3
Derivando implicitamente nossa relação :
Dividindo todo mundo por :
No instante , como temos , , , , , a variação da distância entre o balão e o carro será:
Valeu, galera! Até a próxima! 😉