UFRJ, Sem Campus, Cálculo 1, Listas de C1 - Profº Jair - Primeira Edição V1.3, Questão 4.4.4
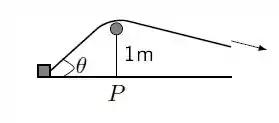
Uma caixa está sendo puxada por uma corda que passa por uma roldana presa a acima do solo. Determine a taxa de variação do ângulo , indicado na figura abaixo, no instante em que a caixa se encontra a do ponto , situado abaixo da roldada, sabendo que a caixa se desloca a .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar a taxa de variação do ângulo, essa taxa pode ser definida por . Mas ele quer o valor da taxa no instante em que a caixa se encontra a uma distância do ponto , sabendo que a caixa se desloca com uma taxa (o sinal é negativo porque a caixa está sendo puxada, diminuindo a distâcia de ).
Então, o que nós vamos fazer é encontrar uma relação entre o ângulo e a distância . A partir dessa relação, derivando implicitamente, vamos obter o valor da taxa .
Vamos lá!
Passo 2
Olhando a nossa figura, a gente percebe que o ângulo entre a caixa e o ponto , pode ser relacionado através dos catetos, e , de modo que teremos:
Daqui, tiramos que se , , o que implica .
Derivando implicitamente a relação que encontramos, obtemos:
Sabendo que , quando e , temos:
Isolando , temos a variação do ângulo:
Valeu, galera! Até a próxima! 😉