UFRJ, Sem Campus, Cálculo 1, Listas de C1 - Profº Jair - Primeira Edição V1.3, Questão 4.4.12
Uma calha horizontal possui de comprimento e tem como seção transversal um triângulo isósceles de de base e de altura conforme mostra a figura abaixo.
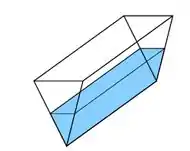
Devido à chuva, a água em seu interior está se elevando. Quão rápido o volume de água em seu interior estará aumentando no instante em que o nível da água for de e estiver aumentando a uma razão de .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar a taxa com que o volume de água no interior do tanque está aumentando.
Vamos chamar de o nível de água e a base do triângulo contendo água. Então, observando a nossa figura, por semelhança de triângulos, temos:
Assim, quando o nível de água for , teremos . O enunciado nos disse que o nível da água está aumentando a uma taxa , mas nós queremos obter a taxa de aumento do volume, que vai ser dado por da base vezes a altura do triângulo vezes , ou seja:
Então, derivando a relação entre base e altura, encontramos . E derivando a relação do volume, com todos os dados considerados, encontramos a taxa de aumento da água .
Vamos lá!
Passo 2
Vamos começar derivando implicitamente a relação entre a base e altura do nível de água, que é :
Como , temos:
Passo 3
Agora vamos derivar a equação do volume, , para encontra a taxa de variação. Usando a regra do produto, temos:
Substituindo , , e , vamos obter:
Que é a variação do volume de água.
Valeu, galera! Até a próxima! 😉