IME, Cálculo 1, 2017, VE1, Q3
Considere um círculo inscrito em triângulo equilátero. Conforme o raio do círculo aumenta, o triângulo também aumenta, de forma que o primeiro esteja sempre inscrito no segundo. Sabendo que o raio do círculo varia a uma taxa de , qual a taxa de variação da área do triângulo quando o raio do círculo alcançar ?
Passo 1
Faaaaaleis vós, consagrados! De primeira, temos que achar o vínculo geométrico entre o triângulo e o círculo para só então utilizar a regra da cadeia para determinar a variação necessária. Avante:
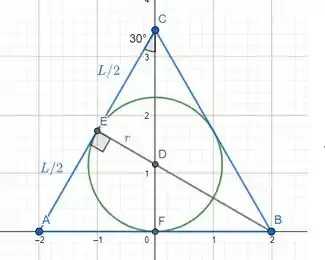
Dessa imagem, temos a área do triângulo e a relação entre e :
Dessa forma, coloquemos em função de :
Passo 2
Agora, derivamos:
Substituindo o valor que temos ficamos com:
Resposta
Exercícios de Livros Relacionados
20. Caminhão na estrada O gráfico a seguir mostra a posição de um caminhão que percorre uma estrada. O caminhão parte em t = 0 e retorna 15 h mais tarde, em t = 15.a. Use a técnica descrita no Exemplo
(a) Encontre a taxa de variação média da área de um círculo em relação ao seu raio r quando r varia de i 2a3i i2a2,5i i i 2a2,1 (b) Encontre a taxa de variação instantânea quando r = 2 (c) Mostre que
O número de células de levedura em uma cultura de laboratório aumenta rapidamente no início, mas eventualmente estabiliza. A população é modelada pela função n = f t = a 1 + b e - 0,7 t Em que t é med
O rendimento total recebido da venda de x carteiras é R x = 200 x - 1 3 x 2 c) Ache o rendimento real da venda da trigésima primeira carteira.
A quantidade de carga Q , em coulombs (C), que passa através de um ponto em um fio até o instante t (medido em segundos) é dada por Q t = t 3 - 2 t 2 + 6 t + 2 Encontre a corrente quando (a) t = 0,5 s