Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Taxa Relacionada

Ver Teoria
Exercício 106123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UNICAMP – Cálculo 1 – Provas Antigas – P2 – 2022.1 - 6ª Diurno – Questão 3

Um corredor corre em uma trajetória circular de raio 100   m a uma velocidade constante de 7   m / s e g . Um outro indivíduo está parado a uma distância de 200   m do centro da pista. Qual a taxa de variação da distância entre os dois quando esta distância for de 200   m ?

Lembre que o comprimento do arco de um setor circular de ângulo θ (em radianos) de uma circunferência de raio r é igual a r θ .

Passo 1

Eaeeee, belezinha??? Vamos juntos entender essa questão aqui!!

Primeiramente, vamos fazer um esquema visual aqui para podermos entender melhor a questão:

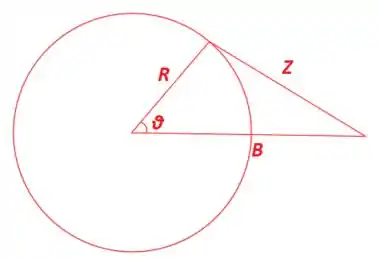
Temos o corredor, percorrendo uma circunferência de raio R = 100 m . À 200 m do centro dessa circunferência, tem um ser humaninho parado (sem nada pra fazer né?!).

Agora precisamos encontrar a equação que descreve esse cenário e, posteriormente, achar a taxa de variação da distância entre esses dois indivíduos!

Passo 2

Assim, podemos utilizar a lei dos cossenos para expressar a distância entre os dois indivíduos:

z 2 = R 2 + B 2 - 2 R B cos ⁡ θ ∴

z 2 = 100 2 + 200 2 - 2 ∙ 100 ∙ 200 ∙ cos ⁡ θ ∴

z 2 = 10 4 ( 5 - 4 cos ⁡ θ )

Passo 3

Agora vamos derivar implicitamente, já que queremos descobrir a taxa de variação:

2 z d z d t = 10 4 4   s e n   θ d θ d t ∴

d z d t = 2 ∙ 10 4 ∙ s e n   θ z d θ d t

O enunciado da questão nos disse que o comprimento do arco de um setor circular ( s ) de ângulo θ (em radianos) de uma circunferência de raio r é igual a r θ . Logo:

d s d t = r d θ d t

Passo 4

Agora, vamos lembrar que:

  • d s d t = 7   m / s e g ;
  • d θ d t = 1 r d s d t = 7 100 ;
  • Distância de 200 metros entre os indivíduos.

Substituindo os dados acima no que a gente encontrou até agora, temos:

200 2 = 100 2 5 - 4 cos ⁡ θ ∴ cos ⁡ θ = 1 4

Sabendo que s e n 2 θ + cos ⁡ θ = 1 , temos que s e n   θ = 15 4 :

d z d t = 2 ∙ 10 4 ∙ 15 4 200 7 100 ∴

d z d t = 7 15 4   m / s

Entendeu direitinho? Responde aee ;)

Resposta

d z d t = 7 15 4   m / s

Exercícios de Livros Relacionados

20. Caminhão na estrada O gráfico a seguir mostra a posição de um caminhão que percorre uma estrada. O caminhão parte em t = 0 e retorna 15 h mais tarde, em t = 15.a. Use a técnica descrita no Exemplo
(a) Encontre a taxa de variação média da área de um círculo em relação ao seu raio r quando r varia de i 2a3i i2a2,5i i i 2a2,1 (b) Encontre a taxa de variação instantânea quando r = 2 (c) Mostre que
O número de células de levedura em uma cultura de laboratório aumenta rapidamente no início, mas eventualmente estabiliza. A população é modelada pela função n = f t = a 1 + b e - 0,7 t Em que t é med
O rendimento total recebido da venda de x carteiras é R x = 200 x - 1 3 x 2 c) Ache o rendimento real da venda da trigésima primeira carteira.
A quantidade de carga Q , em coulombs (C), que passa através de um ponto em um fio até o instante t (medido em segundos) é dada por Q t = t 3 - 2 t 2 + 6 t + 2 Encontre a corrente quando (a) t = 0,5 s