UFRJ, Sem Campus, Cálculo 1, Listas de C1 - Profº Jair - Primeira Edição V1.3, Questão 4.4.6
Dois carros, um dirigindo-se para o leste à razão de e o outro para o sul à razão de , estão viajando em direção à interseção das duas rodovias. À que razão os carros aproximam-se um do outro, no instante em que o primeiro (direção leste) estiver a e o segundo (direção sul) a da interseção?
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar a taxa de variação da distância entre dois carros, cujas posições vamos chamar de e , com origem na interseção entre eles.
Um dos carros tá dirigindo na direção do eixo e sentido para origem, com uma velocidade . E o outro carro tá indo para o sul, na direção do eixo , também com sentido para origem e velocidade . Se a gente chamar de a distância entre eles, a gente consegue visualizar no esquema abaixo que podemos relacionar as variáveis através do teorema de Pitágoras.
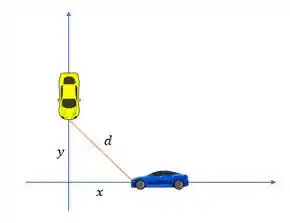
Assim, teremos:
Derivando essa equação e usando os dados do enunciado, vamos obter , que é a derivada de em relação a e representa a taxa de variação da distância entre os carros.
Vamos lá!
Passo 2
Vamos começar pela relação que encontramos na nossa figura:
Derivando implicitamente, temos:
Dividindo todo mundo por :
Mas o enunciado nos deu , . Além disso, ele fala que o primeiro carro (direção leste) está em da origem e o segundo carro (direção sul) está a da interseção. Nesse instante, pela relação do triângulo, temos . Então, substituindo na derivada, temos:
Isolando , vamos obter a razão com que os carros aproximam-se um do outro:
Então, eles estão se aproximando a uma taxa de .
Valeu, galera! Até a próxima! 😉