UFRJ, Sem Campus, Cálculo 1, Listas de C1 - Profº Jair - Primeira Edição V1.3, Questão 4.4.1
Uma escada com de comprimento está apoiada numa parede vertical. Se a base da escada for puxada horizontalmente, afastando-se da parede a , qual a velocidade com que a parte superior da escada estará deslizando ao longo da parede, quando a sua base estiver a da parede?
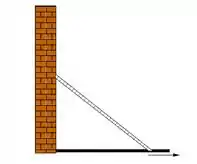
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar a taxa com que a parte superior da escada estará deslizando na parede, quando puxamos sua base a uma taxa de e a base estiver a da parede. Ou seja, queremos descobrir quando e .
A gente pode relacionar essas variáveis através da fórmula de Pitágoras, porque a escada forma um triângulo retângulo com a parede. Assim, derivando implicitamente a relação, a gente consegue com que apareça o termo , que é o valor que queremos encontrar.
Vamos lá!
Passo 2
Como a escada tem um comprimento fixo de e nós queremos saber sua altura quando sua base estiver a da parede, pelo Teorema de Pitágoras, temos:
Isolando :
Então, quando a escada estiver a da parede, ela estará a do chão.
Passo 3
Agora podemos usar o teorema de Pitágoras novamente para encontrar uma relação entre as funções e . Como elas representam os lados do triângulo retângulo formado pela escada e a parede, temos:
Estamos enfatizando que e são funções de . Então, derivando essa relação implicitamente, vamos ter:
Repare que apareceu nosso termo de interesse, que é o . Nós vimos no enunciado que e que em , temos . Então, substituindo na equação, vamos obter:
Simplificando:
Então, o topo da escada desce a uma velocidade de , quando a base da escada está a da parede.
Valeu, galera! Até a próxima! 😉