Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Taxa Relacionada

Ver Teoria
Exercício 144123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UERJ, Sem Campus, Cálculo I, Listas de C1 - Profº Rubens Sucupira - Lista 3, Questão 60

Um farol está a 3   k m de uma praia reta e lança sobre ela um foco de luz. Se o foco gira com velocidade angular de 2   r p m , determine a velocidade com que a luz percorre a praia quando o foco estiver a 2   k m do ponto da praia mais próximo do farol.

Passo 1

Fala, galera! Vamos resolver essa questão!

Nessa questão temos um foco de luz que está girando com uma velocidade angular de 2   r p m e iluminando uma praia. Um esquema desse problema é mostrado na figura a seguir:

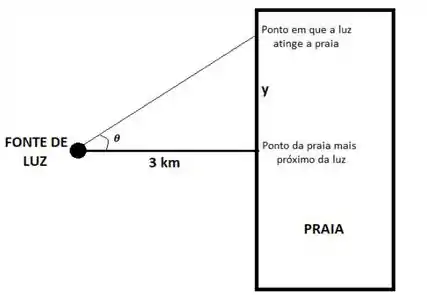
Como a velocidade com que a luz percorre a praia é y ' , queremos achar y ' quando y = 2   k m . Nossa velocidade angular é representada por θ ' = 2   r p m e todas as derivadas vão ser tomadas em relação ao tempo. Assim, olhando o triângulo retângulo da figura, temos:

tan ⁡ θ = y 3 → θ = arctan ⁡ y 3

Essa relação que nós vamos derivar implicitamente em relação ao tempo.

Vamos lá!

Passo 2

Vamos começar derivando a relação encontrada no passo 1 em relação ao tempo:

d θ d t = 1 1 + y 3 2 ∙ y 3 '

d θ d t = 9 9 + y 2 ∙ y ' 3

d θ d t = 3 y ' 9 + y 2

Passo 3

Agora isolando y ' , vamos obter:

y ' = 1 3 d θ d t 9 + y 2 = 1 3 θ ' ( 9 + y 2 )

Antes de substituirmos θ ' e y precisamos converter a velocidade angular de r p m para r a d / s . Para isso, basta multiplicar por 2 π :

θ ' = 2   r p m = 4 π   r a d / s

Assim,

y ' = 1 3 4 π 9 + 2 2 = 4 π 3 ( 9 + 4 )

y ' = 4 π 3 13

y ' = 52 π 3   k m / m i n

Portanto, a velocidade com que a luz percorre a praia quando o foco estiver a 2   k m do ponto da praia mais próximo do farol é de 52 π 3   k m / m i n .

Valeu, galera! Até a próxima! 😉

Resposta

52 π 3   k m / m i n

Exercícios de Livros Relacionados

20. Caminhão na estrada O gráfico a seguir mostra a posição de um caminhão que percorre uma estrada. O caminhão parte em t = 0 e retorna 15 h mais tarde, em t = 15.a. Use a técnica descrita no Exemplo
(a) Encontre a taxa de variação média da área de um círculo em relação ao seu raio r quando r varia de i 2a3i i2a2,5i i i 2a2,1 (b) Encontre a taxa de variação instantânea quando r = 2 (c) Mostre que
O número de células de levedura em uma cultura de laboratório aumenta rapidamente no início, mas eventualmente estabiliza. A população é modelada pela função n = f t = a 1 + b e - 0,7 t Em que t é med
O rendimento total recebido da venda de x carteiras é R x = 200 x - 1 3 x 2 c) Ache o rendimento real da venda da trigésima primeira carteira.
A quantidade de carga Q , em coulombs (C), que passa através de um ponto em um fio até o instante t (medido em segundos) é dada por Q t = t 3 - 2 t 2 + 6 t + 2 Encontre a corrente quando (a) t = 0,5 s